2018年12月13日
2019ヨーロッパ女子数学オリンピック1次選抜(問題4)
こんにちは。
今年もあと半月か・・早いもんだなと毎年言っている。
引き続き、この試験の最終問題です。
見た目シンプルなものほど難しい。

n=3を入れればこれが解の1つとわかるけど、これ以外にあるかどうか?
何となくなさそうだ・・と思えるのだけど、それを示すのが簡単でない。

有理数になるのは√の中が2乗になることで、それには上のa、bの2タイプがある。
bのように、分母分子が平方数でなくても、約分されて平方数になることもあり得る。
なので、問題の式の分数がどんな数で約分できるのか?
これを調べてみた。
続きを読む
今年もあと半月か・・早いもんだなと毎年言っている。
引き続き、この試験の最終問題です。
見た目シンプルなものほど難しい。

n=3を入れればこれが解の1つとわかるけど、これ以外にあるかどうか?
何となくなさそうだ・・と思えるのだけど、それを示すのが簡単でない。

有理数になるのは√の中が2乗になることで、それには上のa、bの2タイプがある。
bのように、分母分子が平方数でなくても、約分されて平方数になることもあり得る。
なので、問題の式の分数がどんな数で約分できるのか?
これを調べてみた。
続きを読む
2018年12月07日
2019ヨーロッパ女子数学オリンピック1次選抜(問題3)
こんにちは。
引き続き、この試験。
興味深い問が揃ってますね。次の問3が最も面白い。

まず具体例を書いてみて、様子を掴むしかないですね。
色のついた部分がX、Y、Zになります。

小さく見積もってX+Y+Z=1になるよう数を入れて行っても、
和は8/3=2.66・・を越えてしまいますね。
どこかを小さくすれば別のところを大きくしないと1以上にならない。
制約がありすぎるので、適当にやれば背理法で示せそうだ・・。
そういう感触なのだけど、ではどう矛盾に持ち込むか・・
このあたりの試行錯誤がなかなか楽しい問い。
続きを読む
引き続き、この試験。
興味深い問が揃ってますね。次の問3が最も面白い。

まず具体例を書いてみて、様子を掴むしかないですね。
色のついた部分がX、Y、Zになります。

小さく見積もってX+Y+Z=1になるよう数を入れて行っても、
和は8/3=2.66・・を越えてしまいますね。
どこかを小さくすれば別のところを大きくしないと1以上にならない。
制約がありすぎるので、適当にやれば背理法で示せそうだ・・。
そういう感触なのだけど、ではどう矛盾に持ち込むか・・
このあたりの試行錯誤がなかなか楽しい問い。
続きを読む
2018年12月03日
2019ヨーロッパ女子数学オリンピック1次選抜(問題2)
こんにちは。
12月に入り、センター試験までひと月とちょっとですね。
入学試験の結果で、これからの人生が大きく変わってしまう。
嫌なもんですね。でも、やるしかないでしょう。
ところで、
いろいろ考えたがどうしても解けず、行き詰ってしまった・・。
こういうときどうするか?

私はこれですね。
4番なんか酷いけど、解けなくて白紙よりはマシでしょう。
引き続き、この試験。

解法の糸口がまったく掴めない問ですね。
まずは三角形、五角形とかで試してみるのがいいです。

この5文字の連立方程式を解くと、結構大変なのだけど解がみな2になる。なので、
2019角形でも同じ結果になりそうだけど、2019文字の連立を解くわけにもいかないし・・。
何かうまい手が必要ですな。
続きを読む
12月に入り、センター試験までひと月とちょっとですね。
入学試験の結果で、これからの人生が大きく変わってしまう。
嫌なもんですね。でも、やるしかないでしょう。
ところで、
いろいろ考えたがどうしても解けず、行き詰ってしまった・・。
こういうときどうするか?

私はこれですね。
4番なんか酷いけど、解けなくて白紙よりはマシでしょう。
引き続き、この試験。

解法の糸口がまったく掴めない問ですね。
まずは三角形、五角形とかで試してみるのがいいです。

この5文字の連立方程式を解くと、結構大変なのだけど解がみな2になる。なので、
2019角形でも同じ結果になりそうだけど、2019文字の連立を解くわけにもいかないし・・。
何かうまい手が必要ですな。
続きを読む
2018年12月01日
2019ヨーロッパ女子数学オリンピック1次選抜(問題1)
こんにちは。
中3生対象の体験教室をしました。
来年塾に入ってもらうよう、いわゆる宣伝のための授業です。

数学を学ぶ意義/数学の勉強の仕方/三石の定理。この3本。
授業後アンケートに答えてもらうのだけど、数学の感想はというと、
・とてもおもしろくてためになる授業でした。
・つまんないと思っていた数学が楽しかったです。
・三石の定理は、とても役に立つと思いました。
嬉しいこと書いてくれてました。おせじでしょうね。
少しでも数学に興味を持ってもらえると、いいです。
ところで、毎年この時期に行われるこういう試験。
面白そうな問が並んでますね。今年も考えてみた。


こういう幾何の問題は、理詰めでは解けないので困るのだけど、
∠AIO=90° ⇔ I が弦の中点になる
とか、同値な条件にすり替えていくのが、1つの考え方ですね。
続きを読む
中3生対象の体験教室をしました。
来年塾に入ってもらうよう、いわゆる宣伝のための授業です。

数学を学ぶ意義/数学の勉強の仕方/三石の定理。この3本。
授業後アンケートに答えてもらうのだけど、数学の感想はというと、
・とてもおもしろくてためになる授業でした。
・つまんないと思っていた数学が楽しかったです。
・三石の定理は、とても役に立つと思いました。
嬉しいこと書いてくれてました。おせじでしょうね。
少しでも数学に興味を持ってもらえると、いいです。
ところで、毎年この時期に行われるこういう試験。
面白そうな問が並んでますね。今年も考えてみた。


こういう幾何の問題は、理詰めでは解けないので困るのだけど、
∠AIO=90° ⇔ I が弦の中点になる
とか、同値な条件にすり替えていくのが、1つの考え方ですね。
続きを読む
2018年04月17日
2017ヨーロッパ女子数学オリンピック1次選抜(問題2)
こんにちは。
新学期が始まり、塾にも新入生が加わった。
初日の生徒は何となく固いのだけど、まあ徐々に打ち解けてきますね。

「解の公式、忘れました!!」
使わないものは、忘れるように人間の頭はできているので・・。
今日忘れた生徒には、来週同じ問を解かせる。しかしまた解けないので、
次の週も同じ問をやらせる。そのうちに嫌でも覚えるでしょう。
反復は大事ですよね。
リクエストにつき、次の難題を・・。

10項くらい書き出していけば何か手掛かりあるだろ・・と思ったが

これ以上やる気がしない・・。
しかしこの時点で、第6項は、第2項と第3項の倍数になっている。
偶然なのか必然なのか、2×3=6だし。そして次の第7項は、
漸化式の形を見ると、2でも5でも割り切れずに1余る。
こんな小さな手掛かりが役に立つのかどうか・・。
続きを読む
新学期が始まり、塾にも新入生が加わった。
初日の生徒は何となく固いのだけど、まあ徐々に打ち解けてきますね。

「解の公式、忘れました!!」
使わないものは、忘れるように人間の頭はできているので・・。
今日忘れた生徒には、来週同じ問を解かせる。しかしまた解けないので、
次の週も同じ問をやらせる。そのうちに嫌でも覚えるでしょう。
反復は大事ですよね。
リクエストにつき、次の難題を・・。

10項くらい書き出していけば何か手掛かりあるだろ・・と思ったが

これ以上やる気がしない・・。
しかしこの時点で、第6項は、第2項と第3項の倍数になっている。
偶然なのか必然なのか、2×3=6だし。そして次の第7項は、
漸化式の形を見ると、2でも5でも割り切れずに1余る。
こんな小さな手掛かりが役に立つのかどうか・・。
続きを読む
2018年01月25日
2018日本数学オリンピック予選(問題10)
こんにちは。
問
A~Hの8人でトーナメント戦を行う。
どのように対戦を組んでも、優勝するのはAかBである。
こうなるような、A~Hの勝敗の表をつくれ。
JMO予選・問題10は大体こんな感じです。4人だけ適当に作ってみると、
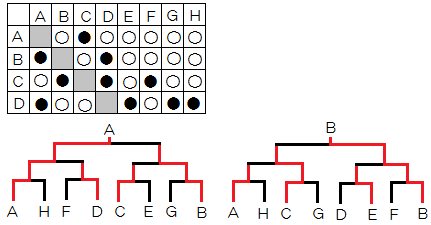
このようにAとBをたくさん勝たせておけば、優勝しやすい。
しかし次のように組むと、3勝しかできないDが優勝してしまう。

A、B以外が優勝しないようにするには、いろいろと条件がありそうですね。
問題はこちら。

「勝敗の組み合わせとしてありうるもの」
これの解釈の仕方が複数あるけど、8人の選手を区別して、誰か2人の勝ち負けが
異なるものはすべて別の組み合わせ、と考えることにします。
そうすれば、発表されている答えと合致するので・・。
続きを読む
問
A~Hの8人でトーナメント戦を行う。
どのように対戦を組んでも、優勝するのはAかBである。
こうなるような、A~Hの勝敗の表をつくれ。
JMO予選・問題10は大体こんな感じです。4人だけ適当に作ってみると、

このようにAとBをたくさん勝たせておけば、優勝しやすい。
しかし次のように組むと、3勝しかできないDが優勝してしまう。

A、B以外が優勝しないようにするには、いろいろと条件がありそうですね。
問題はこちら。

「勝敗の組み合わせとしてありうるもの」
これの解釈の仕方が複数あるけど、8人の選手を区別して、誰か2人の勝ち負けが
異なるものはすべて別の組み合わせ、と考えることにします。
そうすれば、発表されている答えと合致するので・・。
続きを読む
2018年01月23日
2018日本数学オリンピック予選(問題9)
こんにちは。
昨日大雪警報だったけど、夜にはおさまった。
ここより東京のが降ったようだ。雪はほんと困る・・。
JMO予選の続き。

読んでいて途中で嫌になりますね・・。
図に描くとこんな感じになった。

内接円があるときの着目すべき点は、
角の二等分にしるしをつける。
接点での垂直にしるしをつける。
等しい接線にしるしをつける。
この3つですね。
全部使えば、だいたい解けるはず。
続きを読む
昨日大雪警報だったけど、夜にはおさまった。
ここより東京のが降ったようだ。雪はほんと困る・・。
JMO予選の続き。

読んでいて途中で嫌になりますね・・。
図に描くとこんな感じになった。

内接円があるときの着目すべき点は、
角の二等分にしるしをつける。
接点での垂直にしるしをつける。
等しい接線にしるしをつける。
この3つですね。
全部使えば、だいたい解けるはず。
続きを読む
2018年01月22日
2018日本数学オリンピック予選(問題8)
こんにちは。
今週天気が悪いようで、いま雪がしんしんと降り積っている。
なので塾は本日休講・・。
数学Ⅰ「データの分析」について。
センター試験で最もページを割いていて、つまらない上に面倒な分野だと思う。
しかし社会に出てビジネスマンになったとき、きっと役に立つ分野かと思う。
分散とは、データの散らばり具合を示す数。

2通りの分散の公式を、ただ単に暗記するだけでなく、
平均との差が小さいデータほど、分散は小さくなる。
データの2乗の和を考えるとき、分散の公式が使える。
こういうことを知っておくと応用がきく。
JMO予選の続き。

適当に書いてみて手掛かりがないかを探るよりない。
このとき、添え字が同じ式でまとめて考える。

203や195のところをもっと小さくしたいが、どうすればいいか?
右端の和は常に63になるが、このことが関係しているかどうか?
このあたりですかね、考えどころは・・。
続きを読む
今週天気が悪いようで、いま雪がしんしんと降り積っている。
なので塾は本日休講・・。
数学Ⅰ「データの分析」について。
センター試験で最もページを割いていて、つまらない上に面倒な分野だと思う。
しかし社会に出てビジネスマンになったとき、きっと役に立つ分野かと思う。
分散とは、データの散らばり具合を示す数。

2通りの分散の公式を、ただ単に暗記するだけでなく、
平均との差が小さいデータほど、分散は小さくなる。
データの2乗の和を考えるとき、分散の公式が使える。
こういうことを知っておくと応用がきく。
JMO予選の続き。

適当に書いてみて手掛かりがないかを探るよりない。
このとき、添え字が同じ式でまとめて考える。

203や195のところをもっと小さくしたいが、どうすればいいか?
右端の和は常に63になるが、このことが関係しているかどうか?
このあたりですかね、考えどころは・・。
続きを読む
2018年01月20日
2018日本数学オリンピック予選(問題7)
こんにちは。
東京新宿にて。
メニューに1杯なんと3000円の珈琲があった。

一体どんな味がするのだろ?
手前がそれです。ちなみに友人のは700円。
飲み比べてみたのだけど・・
700円の方のがうまかった気がする。残念・・。
JMO予選の続き。

総和が30になるペアは簡単に見つかる。
(1,6) ……差5
(2,7) ……差5
(3,8) ……差5
(4,10) ……差6
(5,11) ……差6
(9,12) ……差3
見方を変えて、各ペアのうちの大きい方だけの6個の和をA、
小さい方だけの6個の和をBとしてみると、
A=6+7+8+10+11+12=54
B=1+2+3+4+5+9=24
A-Bが30になる。
この条件が使えそうですね。
続きを読む
東京新宿にて。
メニューに1杯なんと3000円の珈琲があった。

一体どんな味がするのだろ?
手前がそれです。ちなみに友人のは700円。
飲み比べてみたのだけど・・
700円の方のがうまかった気がする。残念・・。
JMO予選の続き。

総和が30になるペアは簡単に見つかる。
(1,6) ……差5
(2,7) ……差5
(3,8) ……差5
(4,10) ……差6
(5,11) ……差6
(9,12) ……差3
見方を変えて、各ペアのうちの大きい方だけの6個の和をA、
小さい方だけの6個の和をBとしてみると、
A=6+7+8+10+11+12=54
B=1+2+3+4+5+9=24
A-Bが30になる。
この条件が使えそうですね。
続きを読む
2018年01月19日
2018日本数学オリンピック予選(問題6)
こんにちは。
高校入試の図形の問題で、こういう質問が来た。

図の四角形で、辺BC、線分BDの長さを求めよ。
(ラ・サール高)
BCはいいとして、BDはどう解きますか?
トレミーの定理は使用不可とすると、結構めんどい。
JMO予選の続き。上のラ・サールより易しいかもしれない。

問題文がごちゃごちゃしてますが、図を描くと割とシンプルになる。

足して90°になる角を、有効活用せよ
こういう格言があります。
相似な三角形が見つかりそうですね。
続きを読む
高校入試の図形の問題で、こういう質問が来た。

図の四角形で、辺BC、線分BDの長さを求めよ。
(ラ・サール高)
BCはいいとして、BDはどう解きますか?
トレミーの定理は使用不可とすると、結構めんどい。
JMO予選の続き。上のラ・サールより易しいかもしれない。

問題文がごちゃごちゃしてますが、図を描くと割とシンプルになる。

足して90°になる角を、有効活用せよ
こういう格言があります。
相似な三角形が見つかりそうですね。
続きを読む
2018年01月18日
2018日本数学オリンピック予選(問題5)
こんにちは。
随分前に作ったもので、三六オセロといいます。(三六はさぶろくと読む)

子どもが小さい頃、散々対戦したなと、懐かしく思った。
私の子育て論は「親子でよく遊ぶ」というもので、この時間が、
下手な塾に通わすよりずっと意義があると思っていた。
今でもそう思う。
そんな塾に通わす親御さんのおかげで私の仕事があるわけだけど・・。
JMO予選第5問。
これを解くために三六オセロを出してきた。

1個ずつカウントするわけにはいかないし、何か規則性を見つけるか、
または漸化式を作ってしまうか・・。
連続する同じ色の石は、まとめて1個とみなせる
ここが大きなヒントになりますね。
続きを読む
随分前に作ったもので、三六オセロといいます。(三六はさぶろくと読む)

子どもが小さい頃、散々対戦したなと、懐かしく思った。
私の子育て論は「親子でよく遊ぶ」というもので、この時間が、
下手な塾に通わすよりずっと意義があると思っていた。
今でもそう思う。
そんな塾に通わす親御さんのおかげで私の仕事があるわけだけど・・。
JMO予選第5問。
これを解くために三六オセロを出してきた。

1個ずつカウントするわけにはいかないし、何か規則性を見つけるか、
または漸化式を作ってしまうか・・。
連続する同じ色の石は、まとめて1個とみなせる
ここが大きなヒントになりますね。
続きを読む
2018年01月16日
2018日本数学オリンピック予選(問題4)
こんにちは。
センター試験が終わり、私大と国立2次に向けて追い込みですね。
JMO予選の続き。

整数問題で、この手のタイプは大学入試にも出ます。
小さい方から順に、≡1となるものを探す
これしか無いでしょう。
続きを読む
センター試験が終わり、私大と国立2次に向けて追い込みですね。
JMO予選の続き。

整数問題で、この手のタイプは大学入試にも出ます。
小さい方から順に、≡1となるものを探す
これしか無いでしょう。
続きを読む
2018年01月14日
2018日本数学オリンピック予選(問題3)
こんにちは。
センター試験2日目。ここ飯田地方、雪は無く快晴。
これまで地元の受験生の会場は、バスで2時間ほどの信州大だったが、
去年から市内の高校が受験会場となった。これはありがたい。
受験生、健闘を祈る!!
JMO予選の続きです。

中学の知識で解けるのだけど、対角線しか長さがわからないのが
作為的ですね。例えばABの長さをxとして強引に等式を作ると、
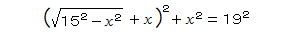
こんな方程式など、解けない・・。
なので、もっと柔軟な発想が必要になりそうだ。
続きを読む
センター試験2日目。ここ飯田地方、雪は無く快晴。
これまで地元の受験生の会場は、バスで2時間ほどの信州大だったが、
去年から市内の高校が受験会場となった。これはありがたい。
受験生、健闘を祈る!!
JMO予選の続きです。

中学の知識で解けるのだけど、対角線しか長さがわからないのが
作為的ですね。例えばABの長さをxとして強引に等式を作ると、
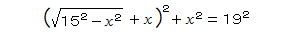
こんな方程式など、解けない・・。
なので、もっと柔軟な発想が必要になりそうだ。
続きを読む
2018年01月13日
2018日本数学オリンピック予選(問題1、2)
こんにちは。
今日明日はセンター試験。
数学は明日ですね。また今年も時間を計って解こうと思う。
その前に、こないだ行われたJMO予選。
解けた問のみUPしようと思います。

これは数学の知識は必要なく、ウォーミングUPの問題。
あまり時間をかけないで見つけたいところです。
続いて問題2

これも書き出していけば、すぐに答えが出ます。
続きを読む
今日明日はセンター試験。
数学は明日ですね。また今年も時間を計って解こうと思う。
その前に、こないだ行われたJMO予選。
解けた問のみUPしようと思います。

これは数学の知識は必要なく、ウォーミングUPの問題。
あまり時間をかけないで見つけたいところです。
続いて問題2

これも書き出していけば、すぐに答えが出ます。
続きを読む
2018年01月10日
2018ヨーロッパ女子数学オリンピック1次選抜(問題4)
こんにちは。
ここ飯田地方、昨日今年初の雪模様だったが、
すっかり溶けて今日は快晴。
こちらの最終問題は、整数解の問だった。

シンプルで実に美しい。
しかしこういう問は得てして難問になる。

どちらの式で行くのがいいのだろ・・?
【策1】 a^n-1、a^k-1をともに因数分解してみる
⇒行き詰る・・
【策2】 a^k-1が2でk回割れるための条件を考える
⇒無理っぽい・・
【策3】 a^k-1をa^n-1で直接割って(余り)=0にする
⇒割れない・・
【策4】 当て推量で答えを出し、これ以外に無いことを示す
⇒この問を解くよりもムズい・・
難航しそうですね・・。
次の因数分解は使えそうなので、書き出しておきます。

(B)の右辺が約分されて、そのあと因数分解できる形になればいい。
そうなることを願って解き進めた・・。
続きを読む
ここ飯田地方、昨日今年初の雪模様だったが、
すっかり溶けて今日は快晴。
こちらの最終問題は、整数解の問だった。

シンプルで実に美しい。
しかしこういう問は得てして難問になる。

どちらの式で行くのがいいのだろ・・?
【策1】 a^n-1、a^k-1をともに因数分解してみる
⇒行き詰る・・
【策2】 a^k-1が2でk回割れるための条件を考える
⇒無理っぽい・・
【策3】 a^k-1をa^n-1で直接割って(余り)=0にする
⇒割れない・・
【策4】 当て推量で答えを出し、これ以外に無いことを示す
⇒この問を解くよりもムズい・・
難航しそうですね・・。
次の因数分解は使えそうなので、書き出しておきます。

(B)の右辺が約分されて、そのあと因数分解できる形になればいい。
そうなることを願って解き進めた・・。
続きを読む
2018年01月09日
2018ヨーロッパ女子数学オリンピック1次選抜(問題1)
こんにちは。
年が明け、また慌ただしい日々が始まりそうだ。
より精進せねばと思う。
引き続きこちらです。大物の問1と問4を悪戦苦闘した。

何というか、洒落た問題と言う感じです。
高校数学Bの「数列」を習っていれば一応解ける問だし、数学的な面白さがある。
元の不等式は因数分解できて、次のようなシンプルな形になります。

つまり元の不等式を満たす数列は、
次の項が、前の項とその前の項の間の整数をとる
ということです。
隣り合う項の差が徐々に小さくなっていき、やがて一致する
というイメージですけど、
・ある項以降が全部一致する
・ある項以降が飛び飛びで一致する
この2つの場合がありますね。
どうやって証明すればいいのか・・悩んだ。
続きを読む
年が明け、また慌ただしい日々が始まりそうだ。
より精進せねばと思う。
引き続きこちらです。大物の問1と問4を悪戦苦闘した。

何というか、洒落た問題と言う感じです。
高校数学Bの「数列」を習っていれば一応解ける問だし、数学的な面白さがある。
元の不等式は因数分解できて、次のようなシンプルな形になります。

つまり元の不等式を満たす数列は、
次の項が、前の項とその前の項の間の整数をとる
ということです。
隣り合う項の差が徐々に小さくなっていき、やがて一致する
というイメージですけど、
・ある項以降が全部一致する
・ある項以降が飛び飛びで一致する
この2つの場合がありますね。
どうやって証明すればいいのか・・悩んだ。
続きを読む
2018年01月08日
2018ヨーロッパ女子数学オリンピック1次選抜(問題3)
こんにちは。
毎年恒例「どんど焼き」という行事。

とにかく寒い朝だった・・。
引き続きこちらを解いていきます。
問題3は図形の問題。これは中学の知識で解けそうだ。

実にシンプルですね。シンプルなほど、実は難しい・・。
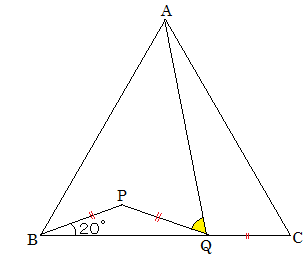
何か補助線を引くと、二等辺ができたり、合同になったり、円に内接したりで、
突然解けることがあるのだけど、どうやればいいか?
APを引く
CPを引く
BPを伸ばす
QPを伸ばす
△PBQを回転させる
いろいろやったがダメだった。なので△PBQを反転させてみた。

四角形ABP´Cが円に内接すればいいのにな・・と願ったが甘かったですね。
しかし、Aを中心にして円を描いてみたら偶然円周上にP´があった。
これで行けそうです。
続きを読む
毎年恒例「どんど焼き」という行事。

とにかく寒い朝だった・・。
引き続きこちらを解いていきます。
問題3は図形の問題。これは中学の知識で解けそうだ。

実にシンプルですね。シンプルなほど、実は難しい・・。

何か補助線を引くと、二等辺ができたり、合同になったり、円に内接したりで、
突然解けることがあるのだけど、どうやればいいか?
APを引く
CPを引く
BPを伸ばす
QPを伸ばす
△PBQを回転させる
いろいろやったがダメだった。なので△PBQを反転させてみた。

四角形ABP´Cが円に内接すればいいのにな・・と願ったが甘かったですね。
しかし、Aを中心にして円を描いてみたら偶然円周上にP´があった。
これで行けそうです。
続きを読む
2018年01月06日
2018ヨーロッパ女子数学オリンピック1次選抜(問題2)
こんにちは。
正月は久々に全オフで、のんびりだった。
大学入試も近いし、過去問を端から解いて行ったのだけど、医学部の数学は
基本的にどこも難しい。答えを出すまでに大変な労力の要る問が多く、
受験生には気の毒に思った。まぁそうしないと点差が付かないのでしょう。
計算力をつけるにはどうすればいいか?
1. ひたすらたくさんこなす
2. ミスを発見する目を持つ
3. 手間を減らす工夫を考える
このあたりですかね。特に2.が弱い人は計算ミスが無くならない。
自分の計算などきっと間違いだ・・と思って進めるのがよいです。
ところでこういう試験を発見したので解いてみました。
正月の間ずっと考えており、やっと全部解けた。4時間で解ける高校生は天才だと思う。
どの問も面白く、思考力を問う良問揃いだと思った。
大問1は解答が大変なので後回しにします。

パズルですね、これは。
問題文の意味がわかりにくいけど、要は、四方が封鎖されるドミノがないようにする、
ということです。
試しに4×4の場合をやってみると、

空マスが少なくなるようにドミノを置く必要がある。4×4の場合は6個が最大っぽい。
実験していくうちに答えは見つかるのだけど、最大であることの証明をしなくては、
得点がもらえない。ここが難なところ。
続きを読む
正月は久々に全オフで、のんびりだった。
大学入試も近いし、過去問を端から解いて行ったのだけど、医学部の数学は
基本的にどこも難しい。答えを出すまでに大変な労力の要る問が多く、
受験生には気の毒に思った。まぁそうしないと点差が付かないのでしょう。
計算力をつけるにはどうすればいいか?
1. ひたすらたくさんこなす
2. ミスを発見する目を持つ
3. 手間を減らす工夫を考える
このあたりですかね。特に2.が弱い人は計算ミスが無くならない。
自分の計算などきっと間違いだ・・と思って進めるのがよいです。
ところでこういう試験を発見したので解いてみました。
正月の間ずっと考えており、やっと全部解けた。4時間で解ける高校生は天才だと思う。
どの問も面白く、思考力を問う良問揃いだと思った。
大問1は解答が大変なので後回しにします。

パズルですね、これは。
問題文の意味がわかりにくいけど、要は、四方が封鎖されるドミノがないようにする、
ということです。
試しに4×4の場合をやってみると、

空マスが少なくなるようにドミノを置く必要がある。4×4の場合は6個が最大っぽい。
実験していくうちに答えは見つかるのだけど、最大であることの証明をしなくては、
得点がもらえない。ここが難なところ。
続きを読む
2017年07月01日
2015日本数学オリンピック予選(問題7)
こんにちは。
2年前のJMO、確か6番まで解いてギブアップした・・。
次の問7を考えてみますか。

意味がわかりづらいけど、格子点を通る平行線が何本あるかという問題。
1つの直線上に格子点が何個あるかが傾きによって違うし、また直線の位置に
よっても変わってくる。このあたりをどうするかが難しい。
STEP1 222本の直線の様子を探る
STEP2 直線Lの傾きを求める
STEP3 問題の答えを数え上げる
この流れで行くしかないか。
300個は多いので、まずは30個で調べてみる。

赤い四角の部分の点は、上下2個で1本とカウントすることになる。
1つの直線上に格子点が3個以上あると面倒なことになるのだけど、
たぶんそれは無いだろうと予測を付けて解くのがいい。
続きを読む
2年前のJMO、確か6番まで解いてギブアップした・・。
次の問7を考えてみますか。

意味がわかりづらいけど、格子点を通る平行線が何本あるかという問題。
1つの直線上に格子点が何個あるかが傾きによって違うし、また直線の位置に
よっても変わってくる。このあたりをどうするかが難しい。
STEP1 222本の直線の様子を探る
STEP2 直線Lの傾きを求める
STEP3 問題の答えを数え上げる
この流れで行くしかないか。
300個は多いので、まずは30個で調べてみる。

赤い四角の部分の点は、上下2個で1本とカウントすることになる。
1つの直線上に格子点が3個以上あると面倒なことになるのだけど、
たぶんそれは無いだろうと予測を付けて解くのがいい。
続きを読む
2017年01月31日
2017日本数学オリンピック予選(問題10)
こんにちは。
東京出張は、高速バスで中央道を通るのだけど、そのバスの中で
いろいろと線を引いて悪戦苦闘した・・。
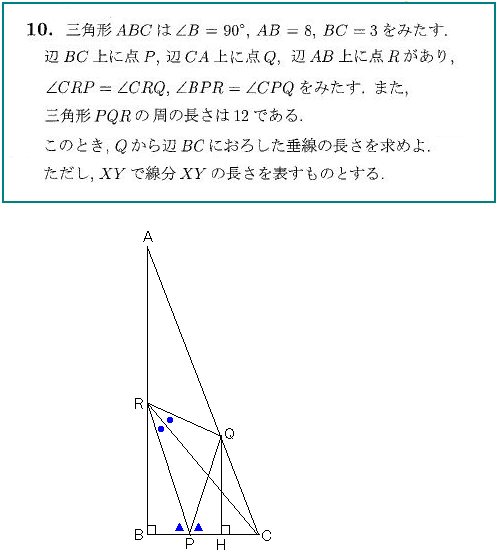
三角形PQRの周の長さが12
これが困った条件で、どう生かすのかが難しい。
折れ線は、まっすぐにのばせ!!
という格言(のようなもの)があります。
これが使えるといいかなと思い、RPとQPをまっすぐに伸ばしたところ、
うまくいった。
続きを読む
東京出張は、高速バスで中央道を通るのだけど、そのバスの中で
いろいろと線を引いて悪戦苦闘した・・。

三角形PQRの周の長さが12
これが困った条件で、どう生かすのかが難しい。
折れ線は、まっすぐにのばせ!!
という格言(のようなもの)があります。
これが使えるといいかなと思い、RPとQPをまっすぐに伸ばしたところ、
うまくいった。
続きを読む





