2018年09月16日
第322回数検1級・1次(第4問)
こんにちは。
更新が滞り、すみません。
「行列」と言う分野。
昔は高校で習っていて1次変換もセットでやったのだけど、今は無い。
次の教科書改訂となる2022年にも、どうやら復活は無いようです。
「複素数平面」が参入してきて押し出された形ですかね・・。
行列、面白いのに残念だ。
7月に行われた数検1級の第4問。

固有値とは、こちら。
ここの説明、難しすぎて読むのが嫌になる・・。
行列式や固有値の問題は過去に沢山出題されてます。
類題はこちら。
これと同じように解けばOKです。
続きを読む
更新が滞り、すみません。
「行列」と言う分野。
昔は高校で習っていて1次変換もセットでやったのだけど、今は無い。
次の教科書改訂となる2022年にも、どうやら復活は無いようです。
「複素数平面」が参入してきて押し出された形ですかね・・。
行列、面白いのに残念だ。
7月に行われた数検1級の第4問。

固有値とは、こちら。
ここの説明、難しすぎて読むのが嫌になる・・。
行列式や固有値の問題は過去に沢山出題されてます。
類題はこちら。
これと同じように解けばOKです。
続きを読む
2018年08月23日
第322回数検1級・1次(第3問)
こんにちは。
母校の中学校では夏期講習が何日かあって、今年も頼まれたので行って来た。

講習と言っても中身はただの自習で、私は生徒の質問に応えるのが仕事だった。
字が汚いせいで、途中で計算がおかしくなっている
ノートを半分に折って使っているので、狭すぎて書きにくい
いろいろですね。
見て回るだけでも随分と面白かったです。
先月行われた数検1級。第3問は空間図形だった。

ベクトルを使った四面体の体積を求める公式があるのだけど、知らなくても解けますね。
しかし、「外積」というものを知らないと結構面倒なことになる。
続きを読む
母校の中学校では夏期講習が何日かあって、今年も頼まれたので行って来た。

講習と言っても中身はただの自習で、私は生徒の質問に応えるのが仕事だった。
字が汚いせいで、途中で計算がおかしくなっている
ノートを半分に折って使っているので、狭すぎて書きにくい
いろいろですね。
見て回るだけでも随分と面白かったです。
先月行われた数検1級。第3問は空間図形だった。

ベクトルを使った四面体の体積を求める公式があるのだけど、知らなくても解けますね。
しかし、「外積」というものを知らないと結構面倒なことになる。
続きを読む
2018年08月10日
第322回数検1級・1次(第2問)
こんにちは。
毎日暑いですね・・。
こちらは高3受験生、夏休みの課題帳。

入試数学演習ⅠAⅡB/使用上の注意
1)解けなくてもすぐに答えを見ないこと。
2)この本の解答を、毎日読書すること。
3)1つの問題を、必ず2回は解くこと。
こんなとこですかね。
20題で入試の基礎力がつくようにと、なかなか考えて作問しました。
冊子見本は、こちら。
プリントして活用するも自由です。間違いあればお知らせください・・。
先月行われた数検1級。
ぼちぼち解いて行きます。

Arcという記号は高校で習わないけど、
逆関数と書いてあるので高校生でも何とかなる。
続きを読む
毎日暑いですね・・。
こちらは高3受験生、夏休みの課題帳。

入試数学演習ⅠAⅡB/使用上の注意
1)解けなくてもすぐに答えを見ないこと。
2)この本の解答を、毎日読書すること。
3)1つの問題を、必ず2回は解くこと。
こんなとこですかね。
20題で入試の基礎力がつくようにと、なかなか考えて作問しました。
冊子見本は、こちら。
プリントして活用するも自由です。間違いあればお知らせください・・。
先月行われた数検1級。
ぼちぼち解いて行きます。

Arcという記号は高校で習わないけど、
逆関数と書いてあるので高校生でも何とかなる。
続きを読む
2018年08月04日
第322回数検1級・1次(第1問)
こんにちは。
今晩、各地でお祭りありますね。
長野びんずる
松本ぼんぼん
飯田りんごん
毎年8月第一土曜でかぶる。どれも変なネーミングだ・・。
先月おこなわれた数検1級。
また解いて行こうと思うけど、つまらない問題はUPしません。
しんどいので・・。

(以前問題掲載の許可を頂いたと思う)
合同式は高校の数学Aで習うので、一応高校レベルの問題。
しかし何をすればいいのか、ちょっと困ってしまうでしょう。
2018n-2が1000の倍数になる
これが合同式の定義で、こういうnを求めればいいわけです。
続きを読む
今晩、各地でお祭りありますね。
長野びんずる
松本ぼんぼん
飯田りんごん
毎年8月第一土曜でかぶる。どれも変なネーミングだ・・。
先月おこなわれた数検1級。
また解いて行こうと思うけど、つまらない問題はUPしません。
しんどいので・・。

(以前問題掲載の許可を頂いたと思う)
合同式は高校の数学Aで習うので、一応高校レベルの問題。
しかし何をすればいいのか、ちょっと困ってしまうでしょう。
2018n-2が1000の倍数になる
これが合同式の定義で、こういうnを求めればいいわけです。
続きを読む
2018年05月17日
第319回数検1級・1次(第2問)
こんにちは。
複素数平面
この分野は高校数学の中に入ったり抜けたりしてますね。
どんな理由があるかわからないが、ずっと入れといてほしい
ですね、面白いので。
複素数の方程式で2乗の場合、次の公式がある。
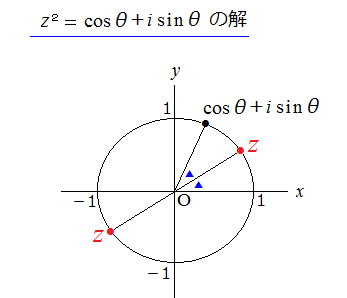
2つの解は原点対称になる。
視覚的に理解できるのが複素数平面の利点かと思う。
先月おこなわれた数検1級。続きです。

上の公式に持ち込めばいいのだけど、
右辺に絶対値がついているのが問題を難しくしている。ここをどう処理するか。
続きを読む
複素数平面
この分野は高校数学の中に入ったり抜けたりしてますね。
どんな理由があるかわからないが、ずっと入れといてほしい
ですね、面白いので。
複素数の方程式で2乗の場合、次の公式がある。

2つの解は原点対称になる。
視覚的に理解できるのが複素数平面の利点かと思う。
先月おこなわれた数検1級。続きです。

上の公式に持ち込めばいいのだけど、
右辺に絶対値がついているのが問題を難しくしている。ここをどう処理するか。
続きを読む
2018年05月09日
第319回数検1級・1次(第1問)
こんにちは。
新規塾生が入り、賑やかになった。
初回の授業はお互い固いです・・。
「数学は好きですか嫌いですか?」
質問の仕方がまずかったか、全員嫌いと答えた。
嫌いな物の勉強をしいられる、こんな苦痛はない。
興味が持てるような、また嫌いで無くなるような授業をせねばと思う。
先月おこなわれた数検1級。また解いて行こうと思います。

(以前問題掲載の了解を頂いた、と思う)
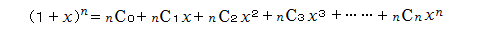
この等式でx=1、n=99を入れれば求めたい式が出てくるけど、
余計な物も出てきますね。その余計な物をどう処理するかが問題。
3の倍数のときだけ残って、あとは消えてほしいのだから、こういうときは
オメガー根
でしょうね。
続きを読む
新規塾生が入り、賑やかになった。
初回の授業はお互い固いです・・。
「数学は好きですか嫌いですか?」
質問の仕方がまずかったか、全員嫌いと答えた。
嫌いな物の勉強をしいられる、こんな苦痛はない。
興味が持てるような、また嫌いで無くなるような授業をせねばと思う。
先月おこなわれた数検1級。また解いて行こうと思います。

(以前問題掲載の了解を頂いた、と思う)
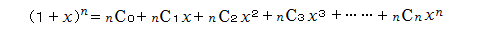
この等式でx=1、n=99を入れれば求めたい式が出てくるけど、
余計な物も出てきますね。その余計な物をどう処理するかが問題。
3の倍数のときだけ残って、あとは消えてほしいのだから、こういうときは
オメガー根
でしょうね。
続きを読む
2018年04月03日
等しい和に分ける方法。
こんにちは。
我が家のソメイヨシノもやっと満開。

樹齢何年かわからない。
毎年少し遅れるが綺麗に咲いてくれる。植えた先祖に感謝です。
ところで、数検HPの過去問のところに面白い問題がありました。

(以前問題掲載はOKと、確か許可を頂いたと思う)
準1級と1級の両方に出題されていた。
こういうnの問題は、すぐに解答を書かずに具体例を調べるのがいいです。

こんな感じになる。この4つでパターンが見えた人は
筋がいい人か、問題の答えを知っている人。
nを4で割った余りに着目する
という発想はすぐに思いつかない。
具体例を調べるうちにその必然性が見えてくる、はず。
続きを読む
我が家のソメイヨシノもやっと満開。

樹齢何年かわからない。
毎年少し遅れるが綺麗に咲いてくれる。植えた先祖に感謝です。
ところで、数検HPの過去問のところに面白い問題がありました。

(以前問題掲載はOKと、確か許可を頂いたと思う)
準1級と1級の両方に出題されていた。
こういうnの問題は、すぐに解答を書かずに具体例を調べるのがいいです。

こんな感じになる。この4つでパターンが見えた人は
筋がいい人か、問題の答えを知っている人。
nを4で割った余りに着目する
という発想はすぐに思いつかない。
具体例を調べるうちにその必然性が見えてくる、はず。
続きを読む
2017年11月11日
第310回数検1級・1次(第3問)
こんにちは。
先月行われた数検1級
第3問は、珍しく空間ベクトルの問だった。

まずは誰でもこういう図をかくでしょう。
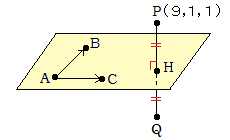
・2つのベクトルに垂直なベクトルを外積で求める
・平面の方程式をx、y、zの1次式で表す
これらを使って解くのが一般的だと思うけど、高校では微妙に範囲外ですね。
しかし、上の2つを使わなくても解くことが可能です。
続きを読む
先月行われた数検1級
第3問は、珍しく空間ベクトルの問だった。

まずは誰でもこういう図をかくでしょう。

・2つのベクトルに垂直なベクトルを外積で求める
・平面の方程式をx、y、zの1次式で表す
これらを使って解くのが一般的だと思うけど、高校では微妙に範囲外ですね。
しかし、上の2つを使わなくても解くことが可能です。
続きを読む
2017年11月11日
第310回数検1級・1次(第2問)
こんにちは。
オイラーの公式
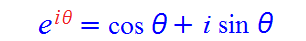
世界で最も美しい公式と言われているとか。
e=2.71828・・・
これの「複素数乗」がなぜsinとcosで表されるのか?
そもそも指数のとこに虚数があることの意味がわからぬ・・
初め、こんな感じだった。

zを式でおいて左辺をsin、cosで表す方法でもいいし、
逆に右辺をeの複素数乗で表す方法でもいい。
後者のがラクですね。
続きを読む
オイラーの公式
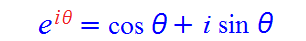
世界で最も美しい公式と言われているとか。
e=2.71828・・・
これの「複素数乗」がなぜsinとcosで表されるのか?
そもそも指数のとこに虚数があることの意味がわからぬ・・
初め、こんな感じだった。

zを式でおいて左辺をsin、cosで表す方法でもいいし、
逆に右辺をeの複素数乗で表す方法でもいい。
後者のがラクですね。
続きを読む
2017年11月09日
第310回数検1級・1次(第1問)
こんにちは。
先月末に行われた数検1級1次。
またぼちぼち解いていきます。
英検や漢検は受けるけど数検は受けない。
私の教え子は皆こうですね、残念だけど。
もっと、皆が当たり前に受検するくらいになってほしいとつね思う。
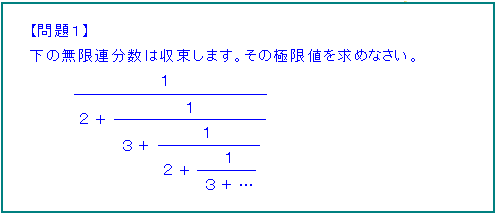
※随分前に数検協会の許可を得て、掲載しています。
「連分数」で検索するといろいろ出てきます。
例えばルート2を連分数で表そうとすると、
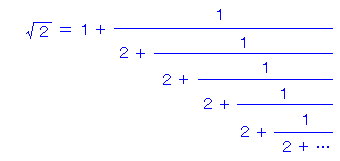
このように実にきれいな式になります。
上の問題は極限値があると言ってくれているので、それをxとおいて
xの方程式を作って解くという方針です。
続きを読む
先月末に行われた数検1級1次。
またぼちぼち解いていきます。
英検や漢検は受けるけど数検は受けない。
私の教え子は皆こうですね、残念だけど。
もっと、皆が当たり前に受検するくらいになってほしいとつね思う。

※随分前に数検協会の許可を得て、掲載しています。
「連分数」で検索するといろいろ出てきます。
例えばルート2を連分数で表そうとすると、
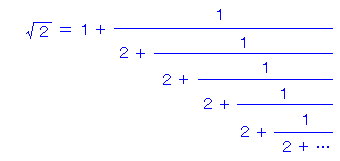
このように実にきれいな式になります。
上の問題は極限値があると言ってくれているので、それをxとおいて
xの方程式を作って解くという方針です。
続きを読む
2017年09月07日
第305回数検1級・1次(第6問)
こんにちは。
塾は今月から授業が1コマ増え、多忙を極めている・・。
写真は高2生、3次方程式を解く授業。

STEP2の割り算には、次の3種類がありますね。
1)ノーマル法
2)組立除法
3)穴埋め法
1)を説明したところ、2)を学校で習ったようだった。なら2)で行くといい。
3)は説明したけど、イマイチ生徒に届かなかった感。
引き続き数検1級。

逆行列は、大学1年の線形代数で習う。
通常の「何とか法」を使えば簡単に出ます。
続きを読む
塾は今月から授業が1コマ増え、多忙を極めている・・。
写真は高2生、3次方程式を解く授業。

STEP2の割り算には、次の3種類がありますね。
1)ノーマル法
2)組立除法
3)穴埋め法
1)を説明したところ、2)を学校で習ったようだった。なら2)で行くといい。
3)は説明したけど、イマイチ生徒に届かなかった感。
引き続き数検1級。

逆行列は、大学1年の線形代数で習う。
通常の「何とか法」を使えば簡単に出ます。
続きを読む
2017年09月02日
第305回数検1級・1次(第5問)
こんにちは。
多忙につきなかなか更新できず・・。
夏休みが終わり、ここ長野県はすでに先週から2学期が始まっている。
生徒が言うには、日本で一番夏休みが短い県が、ここ長野県なのだとか。
ほんとだろうか・・。
引き続き数検1級。
あと残り3問です。何とか次の数検が行われるまでにUPします。

連続型の確率変数の場合、平均と分散は、次の定積分で計算します。
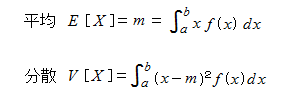
高校数学Bで学習するけど、大学入試では出題外になることが多い。
それほど重要視されていない分野のようです。
続きを読む
多忙につきなかなか更新できず・・。
夏休みが終わり、ここ長野県はすでに先週から2学期が始まっている。
生徒が言うには、日本で一番夏休みが短い県が、ここ長野県なのだとか。
ほんとだろうか・・。
引き続き数検1級。
あと残り3問です。何とか次の数検が行われるまでにUPします。

連続型の確率変数の場合、平均と分散は、次の定積分で計算します。
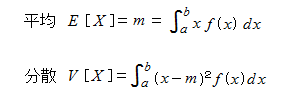
高校数学Bで学習するけど、大学入試では出題外になることが多い。
それほど重要視されていない分野のようです。
続きを読む
2017年08月13日
第305回数検1級・1次(第4問)
こんにちは。
どうも夏バテ気味でいかんですな・・
数検1級の続き。
級数の問題はよく出ますね。

次の形の無限級数を「べき級数」と言います。
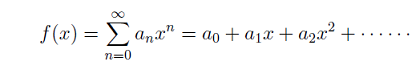
べき級数では、各項を微分してから和を求めることをやってよく、また、
微分した式が収束することと、元の級数が収束することが同値になる。
と専門書に書いてある。なのでこれを認めて利用しよう。
続きを読む
どうも夏バテ気味でいかんですな・・
数検1級の続き。
級数の問題はよく出ますね。

次の形の無限級数を「べき級数」と言います。
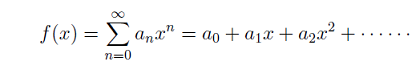
べき級数では、各項を微分してから和を求めることをやってよく、また、
微分した式が収束することと、元の級数が収束することが同値になる。
と専門書に書いてある。なのでこれを認めて利用しよう。
続きを読む
2017年08月11日
第305回数検1級・1次(第3問)
こんにちは。
引き続き数検1級。
第3問は、高校数Bの空間ベクトルの問題。

空間での直線や平面の方程式は、次の形になる。
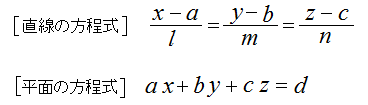
昔の教科書にはバンバンあったけど、最近この形はあまり触れなくなった。
なぜなのか知らないが、知識として知っておいて損は無いです。
続きを読む
引き続き数検1級。
第3問は、高校数Bの空間ベクトルの問題。

空間での直線や平面の方程式は、次の形になる。
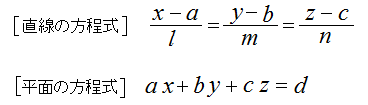
昔の教科書にはバンバンあったけど、最近この形はあまり触れなくなった。
なぜなのか知らないが、知識として知っておいて損は無いです。
続きを読む
2017年08月10日
第305回数検1級・1次(第2問)
こんにちは。
引き続き数検1級。
第2問は珍しく複素数平面だった。

複素数平面は高校の数学Ⅲにあって、この問は高校数学の範囲なのだけど、
最後にある、円を移す条件をどう生かすのかが難しいところです。
複素数平面に出てくる軌跡が円になるものは、次の形と相場が決まっている。

上の等式が与えられた場合は、この形を暗記しておくといいです。
続きを読む
引き続き数検1級。
第2問は珍しく複素数平面だった。

複素数平面は高校の数学Ⅲにあって、この問は高校数学の範囲なのだけど、
最後にある、円を移す条件をどう生かすのかが難しいところです。
複素数平面に出てくる軌跡が円になるものは、次の形と相場が決まっている。

上の等式が与えられた場合は、この形を暗記しておくといいです。
続きを読む
2017年08月09日
第305回数検1級・1次(第1問)
こんにちは。
夏休みまっただ中というところ。
夏期講習が終わり、しばらく私も休養です。
なので、暗礁に乗り上げていた「シニア数学演習」を進めたい。
こう宣言しないとやらないでしょう。やらねば・・。
先月7月に行われた数検1級1次。
ぼちぼち解いていきます。

※随分前に数検協会の許可を得て、掲載しています。
第1問から難問だ。
外側が3乗根なので困ってしまうでしょう。
x+yとxyの対称式
これを意識するのがコツです。
過去問に類題ありますね。こちら。
続きを読む
夏休みまっただ中というところ。
夏期講習が終わり、しばらく私も休養です。
なので、暗礁に乗り上げていた「シニア数学演習」を進めたい。
こう宣言しないとやらないでしょう。やらねば・・。
先月7月に行われた数検1級1次。
ぼちぼち解いていきます。

※随分前に数検協会の許可を得て、掲載しています。
第1問から難問だ。
外側が3乗根なので困ってしまうでしょう。
x+yとxyの対称式
これを意識するのがコツです。
過去問に類題ありますね。こちら。
続きを読む
2017年05月11日
第302回数検1級・1次(問題7)
こんにちは。
数検1級、これがラストです。

インテグラルが3個あって圧倒されますね。
重積分は立体の体積を表していて、その計算方法は、
x、y、zの範囲を定め、1つの文字について順に積分していく
という感じ。
このときの範囲の定め方や積分の順番が非常に厄介で、嫌になる・・。
第190回問題7
これの類題です。今回の方が、やや易しい。
続きを読む
数検1級、これがラストです。

インテグラルが3個あって圧倒されますね。
重積分は立体の体積を表していて、その計算方法は、
x、y、zの範囲を定め、1つの文字について順に積分していく
という感じ。
このときの範囲の定め方や積分の順番が非常に厄介で、嫌になる・・。
第190回問題7
これの類題です。今回の方が、やや易しい。
続きを読む
2017年05月10日
2017年05月09日
第302回数検1級・1次(問題5)
こんにちは。
数検1級、引き続き。

分散=(2乗の平均)-(平均の2乗)
共分散=(Xの偏差)×(Yの偏差)の平均
で求められるのだけど、この問題の場合、XやYは二項分布になるので、
次の公式が使えます。

分散の求め方は高校の範囲内だけど、共分散の公式は高校では習わない。
なぜこんな簡単な式になるのか不思議なのだけど、上から順に式を変形して
行くと、確かに最後の式が出てきます。
続きを読む
数検1級、引き続き。

分散=(2乗の平均)-(平均の2乗)
共分散=(Xの偏差)×(Yの偏差)の平均
で求められるのだけど、この問題の場合、XやYは二項分布になるので、
次の公式が使えます。

分散の求め方は高校の範囲内だけど、共分散の公式は高校では習わない。
なぜこんな簡単な式になるのか不思議なのだけど、上から順に式を変形して
行くと、確かに最後の式が出てきます。
続きを読む
2017年05月07日
第302回数検1級・1次(問題4)
こんにちは。
GWも今日で終わりですか、早いですね。
引き続き、数検1級。

大学1年の線形代数。
「固有値」とか「ハミルトンケーリーの定理」とかを知っていないと解けない。
190回問題4
ここに類似がありますね。
7年前のは固有多項式を求めるステップがあるので良心的だけど、
今回のは意地が悪く、(1)をはずすと全滅になってまう・・。
続きを読む
GWも今日で終わりですか、早いですね。
引き続き、数検1級。

大学1年の線形代数。
「固有値」とか「ハミルトンケーリーの定理」とかを知っていないと解けない。
190回問題4
ここに類似がありますね。
7年前のは固有多項式を求めるステップがあるので良心的だけど、
今回のは意地が悪く、(1)をはずすと全滅になってまう・・。
続きを読む





