2025年01月29日
2025日本数学オリンピック予選(問題5)
こんにちは。
行き付けの店に。

ボトルをキープして飲む。
こういうの若い頃は無かったな、金なかったし・・。
受験のシーズン。
そろそろ私の会社も忙しくなり、酒飲む時間も無くなりそうだ。
JMOの続きです。

図が入り組んでいて複雑ですな。どうすれば解けるのか?その発見が難しい。
形からして「メネラウスの定理」かな?と思ったが、求める比の形はその定理には出てこない。
でもひとまずは、BCとCDを文字で置いて、他の線分をその文字で表すことを考えます。
続きを読む
行き付けの店に。

ボトルをキープして飲む。
こういうの若い頃は無かったな、金なかったし・・。
受験のシーズン。
そろそろ私の会社も忙しくなり、酒飲む時間も無くなりそうだ。
JMOの続きです。

図が入り組んでいて複雑ですな。どうすれば解けるのか?その発見が難しい。
形からして「メネラウスの定理」かな?と思ったが、求める比の形はその定理には出てこない。
でもひとまずは、BCとCDを文字で置いて、他の線分をその文字で表すことを考えます。
続きを読む
2025年01月19日
2025日本数学オリンピック予選(問題4)
こんにちは。
大学入学共通テスト、終わったようですね。
数1A、数2Bともやや易化とのこと。
どこかにUPされ次第、解いていくことにします。
JMOの続き。

例えば、58と言う数。
58÷2=29あまり0
58÷3=19あまり1
58÷4=14あまり2
58÷5=11あまり3
58÷6=9 あまり4
となって、条件を満たします。
余りの方を先に決めて、それに見合うNを探す方法がよいです。
例えば58に2を足せば、2、3、4、5、6のどれでも割り切れる。
こういう都合のよい数を見つけると早いです。
続きを読む
大学入学共通テスト、終わったようですね。
数1A、数2Bともやや易化とのこと。
どこかにUPされ次第、解いていくことにします。
JMOの続き。

例えば、58と言う数。
58÷2=29あまり0
58÷3=19あまり1
58÷4=14あまり2
58÷5=11あまり3
58÷6=9 あまり4
となって、条件を満たします。
余りの方を先に決めて、それに見合うNを探す方法がよいです。
例えば58に2を足せば、2、3、4、5、6のどれでも割り切れる。
こういう都合のよい数を見つけると早いです。
続きを読む
2025年01月18日
2025日本数学オリンピック予選(問題3)
こんにちは。
引き続きJMO予選。

10×10のマス目

これに、次のピースを置くという問題。

パズルのようにいろんな並べ方がありそうで大変だな・・
と思ったが、どうも規則性があって割と簡単だった。
続きを読む
引き続きJMO予選。

10×10のマス目

これに、次のピースを置くという問題。

パズルのようにいろんな並べ方がありそうで大変だな・・
と思ったが、どうも規則性があって割と簡単だった。
続きを読む
2025年01月17日
2025日本数学オリンピック予選(問題1・2)
こんにちは。
明日から大学入学共通テストですね。
今年から数1Aの範囲が変わって、整数論の分野が消え、
確率、幾何が必須となってしまった。
幾何は勉強しにくい分野だし、点が取りにくい感じあるかな。
変わって、先週行われたJMO予選。
毎年解ける問だけ解いているけど、毎年沼にハマって、
仕事がおろそかになる。今日もそうだった。

全12問の中では易しいのだけど、どちらも数え上げなので、漏れが怖いです。
第1問では真ん中の数を先に決めるよりも、
「7」がどこに来るか?7と隣り合う数がどう入るか?を考える方がラクかな。
第2問は2025が平方数なので、2数の積が平方数になる条件を考えます。
続きを読む
明日から大学入学共通テストですね。
今年から数1Aの範囲が変わって、整数論の分野が消え、
確率、幾何が必須となってしまった。
幾何は勉強しにくい分野だし、点が取りにくい感じあるかな。
変わって、先週行われたJMO予選。
毎年解ける問だけ解いているけど、毎年沼にハマって、
仕事がおろそかになる。今日もそうだった。

全12問の中では易しいのだけど、どちらも数え上げなので、漏れが怖いです。
第1問では真ん中の数を先に決めるよりも、
「7」がどこに来るか?7と隣り合う数がどう入るか?を考える方がラクかな。
第2問は2025が平方数なので、2数の積が平方数になる条件を考えます。
続きを読む
2024年01月25日
2024日本数学オリンピック予選(問題9)
こんにちは。
引き続きJMOです。

図形の問題。これは激ムズだった。

線分DFは四角形の内部の線なので、なかなか求めにくい。
三角DFCとDAEが相似なのはすぐ見えるけど、どちらの辺も
長さが1つもわからないのだから困る。
線を足してみますか。
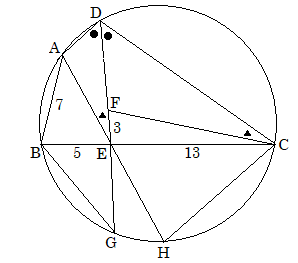
これで何とか行けるか?と思ったけど、手掛かりがつかめない。
それどころか、余計難しくなっている。
では、これならどうか?

黄色の三角形が三角DGCと相似なことと、二等分線の比が使えるので、
図のxが求められそうだ。
どうやらこれが突破口ですね。
続きを読む
引き続きJMOです。

図形の問題。これは激ムズだった。

線分DFは四角形の内部の線なので、なかなか求めにくい。
三角DFCとDAEが相似なのはすぐ見えるけど、どちらの辺も
長さが1つもわからないのだから困る。
線を足してみますか。

これで何とか行けるか?と思ったけど、手掛かりがつかめない。
それどころか、余計難しくなっている。
では、これならどうか?

黄色の三角形が三角DGCと相似なことと、二等分線の比が使えるので、
図のxが求められそうだ。
どうやらこれが突破口ですね。
続きを読む
2024年01月23日
2024日本数学オリンピック予選(問題8)
こんにちは。
引き続きJMOです。

1から2024までの関数の値か・・これは大変だなと言う感。
こういう問はとりあえず0とか1を代入して小さい値を求めます。
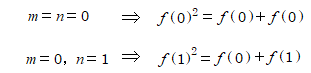
この結果、f(0)とf(1)が決まりそうだ。
あとは、mとnの一方を残した等式を作って、
そこから規則が見つかればラッキー。と言う感じでやります。
続きを読む
引き続きJMOです。

1から2024までの関数の値か・・これは大変だなと言う感。
こういう問はとりあえず0とか1を代入して小さい値を求めます。
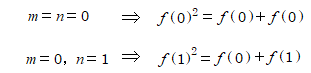
この結果、f(0)とf(1)が決まりそうだ。
あとは、mとnの一方を残した等式を作って、
そこから規則が見つかればラッキー。と言う感じでやります。
続きを読む
2024年01月21日
2024日本数学オリンピック予選(問題7)
こんにちは。
引き続きJMOです。

どうやって解くか?
・元の式を平方完成しようと試みる
・元の式を =M^2 とおいて、式変形する
・aに1、2、3を入れて解の規則を調べる
こういうのではうまく行かないですね。そんなに甘くない。
元の式にpの項が無いこと、定数項が1であること、
これがすごいヒントであって、

このように決めつけていいかどうかは後で考えるとして、
ひとまずこれが突破口になる。
続きを読む
引き続きJMOです。

どうやって解くか?
・元の式を平方完成しようと試みる
・元の式を =M^2 とおいて、式変形する
・aに1、2、3を入れて解の規則を調べる
こういうのではうまく行かないですね。そんなに甘くない。
元の式にpの項が無いこと、定数項が1であること、
これがすごいヒントであって、

このように決めつけていいかどうかは後で考えるとして、
ひとまずこれが突破口になる。
続きを読む
2024年01月18日
2024日本数学オリンピック予選(問題6)
こんにちは。
毎日、北風が冷たい。
引き続きJMOです。

図を描くとこうなる。

2つの円が接すると書いてあり、これらの円が点Eで交わるのだから、
この点Eで外接するはずです。
図形の問で最初に調べることといえば、このあたり。
1 等しい辺や角に印をつける
2 合同な三角形はあるか?
3 相似な三角形はあるか?
4 平行線はあるか?
5 二等分線はあるか?
6 内接四角形はあるか?
上の図では、ABとCFが平行に見えるけどたぶん違う。
でも何となく△ABEと△CFEが相似になりそうですね。
あと、2円が接するときの策としては、
共通接線を引いてみる
これもやってみると何か手掛かりがつかめるかもしれない。
実際、やってみたら効果大だった。
続きを読む
毎日、北風が冷たい。
引き続きJMOです。

図を描くとこうなる。

2つの円が接すると書いてあり、これらの円が点Eで交わるのだから、
この点Eで外接するはずです。
図形の問で最初に調べることといえば、このあたり。
1 等しい辺や角に印をつける
2 合同な三角形はあるか?
3 相似な三角形はあるか?
4 平行線はあるか?
5 二等分線はあるか?
6 内接四角形はあるか?
上の図では、ABとCFが平行に見えるけどたぶん違う。
でも何となく△ABEと△CFEが相似になりそうですね。
あと、2円が接するときの策としては、
共通接線を引いてみる
これもやってみると何か手掛かりがつかめるかもしれない。
実際、やってみたら効果大だった。
続きを読む
2024年01月16日
2024日本数学オリンピック予選(問題5)
こんにちは。
本日届いた。

バンドを結成してデビューを夢見ていた若い頃もあったけど、ヘタ過ぎた。
当時のメンバーから練習を再開しないかと年賀状が来て、それで購入となった。
送られてきた譜面の先頭には、こう書かれてある。

うう・・いきなりムズい。
自主練をせねば・・。
引き続きJMOです。

左辺は見づらいけど、10個のガウス記号による整数値の積です。
右辺を分数で書いて順番を直すと、こうなる。

ずいぶん特徴のある形になった。両辺の左から順番に等しくなればいいんでは?
そんなので解けるかどうかわからぬが、まずはそう解釈するのが第一歩です。
続きを読む
本日届いた。

バンドを結成してデビューを夢見ていた若い頃もあったけど、ヘタ過ぎた。
当時のメンバーから練習を再開しないかと年賀状が来て、それで購入となった。
送られてきた譜面の先頭には、こう書かれてある。

うう・・いきなりムズい。
自主練をせねば・・。
引き続きJMOです。

左辺は見づらいけど、10個のガウス記号による整数値の積です。
右辺を分数で書いて順番を直すと、こうなる。

ずいぶん特徴のある形になった。両辺の左から順番に等しくなればいいんでは?
そんなので解けるかどうかわからぬが、まずはそう解釈するのが第一歩です。
続きを読む
2024年01月14日
2024日本数学オリンピック予選(問題4)
こんにちは。
大学入学共通テスト、行われたようです。
数学は今日ですか。問がUPされ次第解いてみます。
引き続きJMOです。

これを解く場合、まずはこういう図を描くでしょうね。
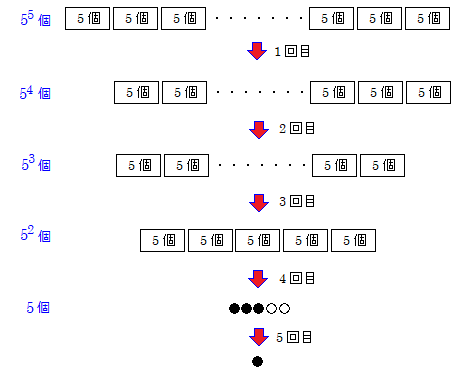
黒石の最小数を求めるので、白石をなるべく多くすることを考えて、
下から計算するといいです。
続きを読む
大学入学共通テスト、行われたようです。
数学は今日ですか。問がUPされ次第解いてみます。
引き続きJMOです。

これを解く場合、まずはこういう図を描くでしょうね。

黒石の最小数を求めるので、白石をなるべく多くすることを考えて、
下から計算するといいです。
続きを読む
2024年01月12日
2024日本数学オリンピック予選(問題3)
こんにちは。
方べきの定理

右の等式は、左の図のCとDが一致したと考えれば納得が行く。
数学の公式というものはただ暗記するだけでなくて、
こういう形ならこの定理が使える
というパターンをいろいろ知っておくことが大事で、
これが思考の幅を広げる効果につながる。と思う。

図を見て、「方べきだな~」と思える人はなかなか。
続きを読む
方べきの定理

右の等式は、左の図のCとDが一致したと考えれば納得が行く。
数学の公式というものはただ暗記するだけでなくて、
こういう形ならこの定理が使える
というパターンをいろいろ知っておくことが大事で、
これが思考の幅を広げる効果につながる。と思う。

図を見て、「方べきだな~」と思える人はなかなか。
続きを読む
2024年01月11日
2024日本数学オリンピック予選(問題1・2)
こんにちは。
外は、今日も風が冷たい。
毎年この時期に行われているようです、この予選会。
高校生以下が参加でき、一応高校までの知識で解けるとのこと。
しかし実際はかなりムズい。
数学の問が解けないとき、どうするか?

このあたりですかね。
今年も解けた問のみUPします。

最初はそれほど難ではないです。
2番は、端から探せば2個くらいすぐに見つかる。
続きを読む
外は、今日も風が冷たい。
毎年この時期に行われているようです、この予選会。
高校生以下が参加でき、一応高校までの知識で解けるとのこと。
しかし実際はかなりムズい。
数学の問が解けないとき、どうするか?

このあたりですかね。
今年も解けた問のみUPします。

最初はそれほど難ではないです。
2番は、端から探せば2個くらいすぐに見つかる。
続きを読む
2020年02月12日
2020日本数学オリンピック予選(問題9)
こんにちは。
東京に越して10か月ほど経った。
必死に会社を経営してきたけど、儲からないですね・・。
まだまだ甘いか。もっと努力せねば。
都内、うまい珈琲店を探し歩いて半年が過ぎた。
最近見つけたのは神保町。地下にある薄暗く古風な感じで、
テーブルはガタガタするし、暗いので数学の問も解きづらい。

コーヒー通がうなるブレンド。
ネットにこう書かれてあったけど、ほんとにうなった。
薄暗く古風なのも、慣れると落ち着く。
おかげで次の問がやっと解けたところ。

ネットに解答が落ちているかと探したけど、無いですね。
勝手に関数をつくり、m、nに適当な数を入れて調べます。
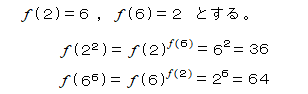
初めこれが答えかなと思ったけど、そう甘くないです。
どういう風に6の6乗を調べて、どうやって最小を見つけるのか?
理詰めでは解けないですね。なので、小さい方から順に調べることにしました。
続きを読む
東京に越して10か月ほど経った。
必死に会社を経営してきたけど、儲からないですね・・。
まだまだ甘いか。もっと努力せねば。
都内、うまい珈琲店を探し歩いて半年が過ぎた。
最近見つけたのは神保町。地下にある薄暗く古風な感じで、
テーブルはガタガタするし、暗いので数学の問も解きづらい。

コーヒー通がうなるブレンド。
ネットにこう書かれてあったけど、ほんとにうなった。
薄暗く古風なのも、慣れると落ち着く。
おかげで次の問がやっと解けたところ。

ネットに解答が落ちているかと探したけど、無いですね。
勝手に関数をつくり、m、nに適当な数を入れて調べます。
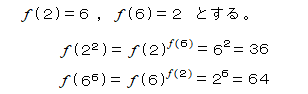
初めこれが答えかなと思ったけど、そう甘くないです。
どういう風に6の6乗を調べて、どうやって最小を見つけるのか?
理詰めでは解けないですね。なので、小さい方から順に調べることにしました。
続きを読む
2020年02月03日
2020日本数学オリンピック予選(問題6)
こんにちは。
東京で久々家族皆そろったので、マンションから近い
深大寺(ジンダイジ)というお寺に行きました。
観光スポットのようで、賑やかだった。

このように、お参りするにも長い列に並んだ。
出店が並ぶ中に陶芸の店があって、絵を描くと焼いてくれる
というので、お皿に絵を描いた。

センス無いねぇ
と皆が言う・・。
JMOはなかなか進まない。
解けた問からUPしていきます。
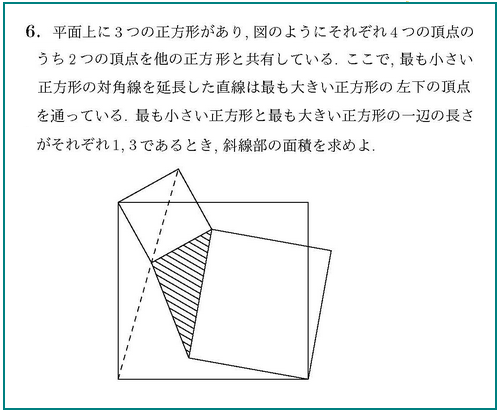
これは中学の幾何で解ける問題。
斜線の三角形をそのまま考えるのでなく、うまく図形をずらして
求めやすいものに置き換える感じです。その前に合同な三角形とか、
図の中に隠れた性質を見つける必要があって、そこがムズい。
続きを読む
東京で久々家族皆そろったので、マンションから近い
深大寺(ジンダイジ)というお寺に行きました。
観光スポットのようで、賑やかだった。

このように、お参りするにも長い列に並んだ。
出店が並ぶ中に陶芸の店があって、絵を描くと焼いてくれる
というので、お皿に絵を描いた。

センス無いねぇ
と皆が言う・・。
JMOはなかなか進まない。
解けた問からUPしていきます。

これは中学の幾何で解ける問題。
斜線の三角形をそのまま考えるのでなく、うまく図形をずらして
求めやすいものに置き換える感じです。その前に合同な三角形とか、
図の中に隠れた性質を見つける必要があって、そこがムズい。
続きを読む
2020年01月27日
2020日本数学オリンピック予選(問題3・4)
こんにちは。
私が運営する某スポーツクラブの新年会。

ずっと続けてきて今年で15年目になるかな。
いろんな人の協力のおかげなのだろうけど、
大半は私の努力かな。そう言いたいところです。
根気 勇気
が大事だよと言ってきたけど、何をするにも当てはまるかと思う。
これが自然に持てるような人になってほしい、とつね思う。
毎年この時期に行われるJMO予選。
じっくり考えたいのだけど本業が忙しい・・。

どちらも端から書き出していけば、やがて解が出ますね。
あまり面白くないです。
続きを読む
私が運営する某スポーツクラブの新年会。

ずっと続けてきて今年で15年目になるかな。
いろんな人の協力のおかげなのだろうけど、
大半は私の努力かな。そう言いたいところです。
根気 勇気
が大事だよと言ってきたけど、何をするにも当てはまるかと思う。
これが自然に持てるような人になってほしい、とつね思う。
毎年この時期に行われるJMO予選。
じっくり考えたいのだけど本業が忙しい・・。

どちらも端から書き出していけば、やがて解が出ますね。
あまり面白くないです。
続きを読む
2020年01月16日
2020日本数学オリンピック予選(問題1・2)
こんにちは。
今年で終了となるセンター試験は明後日。
数学は計算力重視で時間攻めという試験で、つまらなかった。
共通テストに代われば面白くなるかなと期待していたのだけど、
試行テストを見た限り、(こちら)
暗雲立ち込めるという感・・。
毎年この時期に行われるJMO予選。
面白い問が出てます。解けそうなもののみ解いてみますか。
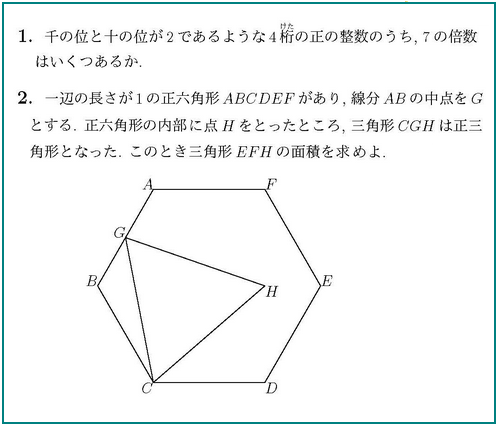
問1
7の倍数の見つけ方は知らないので、さてどうしますか?
位を別々にして7で割って余りを集める、という感じです。
問2
△EFHの底辺をEFとするか、HEとするか?
いくつか解き方がありそうです。
続きを読む
今年で終了となるセンター試験は明後日。
数学は計算力重視で時間攻めという試験で、つまらなかった。
共通テストに代われば面白くなるかなと期待していたのだけど、
試行テストを見た限り、(こちら)
暗雲立ち込めるという感・・。
毎年この時期に行われるJMO予選。
面白い問が出てます。解けそうなもののみ解いてみますか。

問1
7の倍数の見つけ方は知らないので、さてどうしますか?
位を別々にして7で割って余りを集める、という感じです。
問2
△EFHの底辺をEFとするか、HEとするか?
いくつか解き方がありそうです。
続きを読む
2019年01月21日
2019日本数学オリンピック予選(問題5)
こんにちは。
センター試験が終わりました。
ゆうべ時間を測って解いてみたのだけど、いくつかミスったし、
数1Aなんか時間オーバーだった・・。
数1A 第4問の整数問題は、
49 x-23 y=1
これの整数解を求める問から始まるのだけど、
教科書通り「ユークリッドの互除法」を使うのは手間かかりますね。
49x ≡ 1 (mod23)
これを解く方法を是非習得すべき。
引き続きJMO予選。
ちょうど整数解の問でした。

類題が青チャートにもありますね。
97x+32=100y+33=103z+34
これを解けばいい。
しかし係数が大きくて大変なので、先ほど言った合同式を使うのがいいです。
続きを読む
センター試験が終わりました。
ゆうべ時間を測って解いてみたのだけど、いくつかミスったし、
数1Aなんか時間オーバーだった・・。
数1A 第4問の整数問題は、
49 x-23 y=1
これの整数解を求める問から始まるのだけど、
教科書通り「ユークリッドの互除法」を使うのは手間かかりますね。
49x ≡ 1 (mod23)
これを解く方法を是非習得すべき。
引き続きJMO予選。
ちょうど整数解の問でした。

類題が青チャートにもありますね。
97x+32=100y+33=103z+34
これを解けばいい。
しかし係数が大きくて大変なので、先ほど言った合同式を使うのがいいです。
続きを読む
2019年01月19日
2019日本数学オリンピック予選(問題4)
こんにちは。
正五角形の内角や対角線の性質は、次のようになる。

あまり入試で見かけないけど、知識として知っておくといいです。
引き続きJMO予選。
第4問は中学の幾何の問題。

うまい補助線を引いて、相似比に持ち込む感じです。
続きを読む
正五角形の内角や対角線の性質は、次のようになる。

あまり入試で見かけないけど、知識として知っておくといいです。
引き続きJMO予選。
第4問は中学の幾何の問題。

うまい補助線を引いて、相似比に持ち込む感じです。
続きを読む
2019年01月18日
2019日本数学オリンピック予選(問題3)
こんにちは。
引き続きJMO予選。
第3問はパズルのように見えて、実は厄介な場合の数の計算。

OKな並べ方を書き出すと、例えば次のよう。

両端の数1と9がどこに来るのか?
まずはこれを調べてみたところ、アのように両方カドに来る場合と、
イのように片方が中に入る場合がある。
なのでその基準で場合分けですね。
続きを読む
引き続きJMO予選。
第3問はパズルのように見えて、実は厄介な場合の数の計算。

OKな並べ方を書き出すと、例えば次のよう。

両端の数1と9がどこに来るのか?
まずはこれを調べてみたところ、アのように両方カドに来る場合と、
イのように片方が中に入る場合がある。
なのでその基準で場合分けですね。
続きを読む
2019年01月17日
2019日本数学オリンピック予選(問題1・2)
こんにちは。
毎年この時期に行われるJMO予選。
今年も解けた問のみUPしようと思います。

31が素数なので、左辺を因数分解すればxがすぐ出ますね。

パズルのような問題。
1桁の素数は2、3、5、7だから、百の位と一の位を決めてしまえば、
あとは1つずつ調べて行けばいい。それほど大変ではないです。
続きを読む
毎年この時期に行われるJMO予選。
今年も解けた問のみUPしようと思います。

31が素数なので、左辺を因数分解すればxがすぐ出ますね。

パズルのような問題。
1桁の素数は2、3、5、7だから、百の位と一の位を決めてしまえば、
あとは1つずつ調べて行けばいい。それほど大変ではないです。
続きを読む




