2024年10月04日
組合せnCrの公式。
こんにちは。
残業中。ふう・・ひと息です。
このところやっと涼しくなってきた感。
東京の夏は暑いな。人込みと暑さ。これが困る・・
それ以外は便利で住みやすいのだけど。
数学の話。

期待値を計算していたらこういう式が出てきた。
これ、計算できるのだろうか?10個の項をそれぞれ書いて
計算するのでなく、1つのCの式にしたい。
k倍が邪魔なので、これを無くしてΣnCrという形にするというテクを使う。
組合せnCrの公式というと、次の(1)(2)は有名で、(3)は見かけないけど、
この(3)を使うとうまく行きます。
答 10×20C11

左辺か右辺を変形していけば証明できるけど、そうでなく、組合せの総数を
考えることで示せないか?それを考えてみました。
続きを読む
残業中。ふう・・ひと息です。
このところやっと涼しくなってきた感。
東京の夏は暑いな。人込みと暑さ。これが困る・・
それ以外は便利で住みやすいのだけど。
数学の話。

期待値を計算していたらこういう式が出てきた。
これ、計算できるのだろうか?10個の項をそれぞれ書いて
計算するのでなく、1つのCの式にしたい。
k倍が邪魔なので、これを無くしてΣnCrという形にするというテクを使う。
組合せnCrの公式というと、次の(1)(2)は有名で、(3)は見かけないけど、
この(3)を使うとうまく行きます。
答 10×20C11

左辺か右辺を変形していけば証明できるけど、そうでなく、組合せの総数を
考えることで示せないか?それを考えてみました。
続きを読む
2024年09月21日
玉を取り出す確率。
こんにちは。
会社によくセールスが来るのだけど、
「珈琲の機械を置きませんか?」
という人が来た。
私は珈琲バカ。一日に何杯も飲むのだけど、
「ネルドリップが一番うまい」
と言ったら、その人ネルドリップを知らないと言う。

こういうやつです。知っててほしかったな。
今日は条件付き確率の問を1つ。

最近you tubeで観た問なのだけど、それは合計が10でなく文字のNだった。
その動画の解き方が何だかよくわからなかったな・・。
直感だと、次の3通りがありますね。
1)何回取り出しても五分五分なので、答えは50%
2)1回目が赤だから、赤が有利。答えは50%よりやや高い。
3)1回目が赤だから、赤が1個減って白が有利。答えは50%よりやや低い。
どれだと思います?
こういう直感も案外大事なことかと思う。
ではどう解くか?条件付き確率なので、教科書通りの設定です。
A:箱から1個取り出したらそれが赤玉である
B:箱から2個目を取り出したらそれが赤玉である
すると、こういう式になる。
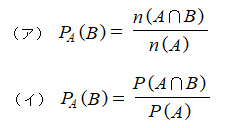
2つのうちやりやすい方を使えばいいけど、(ア)で行けるならそれがいいです。
これ、初期設定がわからないのでAもBも何通りか困ってしまいますね。
問の最後に書いた但し書きに合わせて11パターン全部を考えることになります。
続きを読む
会社によくセールスが来るのだけど、
「珈琲の機械を置きませんか?」
という人が来た。
私は珈琲バカ。一日に何杯も飲むのだけど、
「ネルドリップが一番うまい」
と言ったら、その人ネルドリップを知らないと言う。

こういうやつです。知っててほしかったな。
今日は条件付き確率の問を1つ。

最近you tubeで観た問なのだけど、それは合計が10でなく文字のNだった。
その動画の解き方が何だかよくわからなかったな・・。
直感だと、次の3通りがありますね。
1)何回取り出しても五分五分なので、答えは50%
2)1回目が赤だから、赤が有利。答えは50%よりやや高い。
3)1回目が赤だから、赤が1個減って白が有利。答えは50%よりやや低い。
どれだと思います?
こういう直感も案外大事なことかと思う。
ではどう解くか?条件付き確率なので、教科書通りの設定です。
A:箱から1個取り出したらそれが赤玉である
B:箱から2個目を取り出したらそれが赤玉である
すると、こういう式になる。
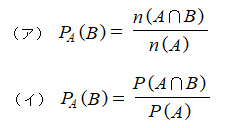
2つのうちやりやすい方を使えばいいけど、(ア)で行けるならそれがいいです。
これ、初期設定がわからないのでAもBも何通りか困ってしまいますね。
問の最後に書いた但し書きに合わせて11パターン全部を考えることになります。
続きを読む
2024年08月18日
夏休み課題その5
こんにちは。
夏休み。
私の会社は今日までで9連休。
自分の会社なので自分で休みを決めたのだけど、長かったな。
休みボケ。仕事モードになるのに時間がかかりそうだ・・。
今日は課題の5。確率を考えてみますか。

よくある間違いを2つ挙げました。
それぞれ明確な誤りの理由があって、指摘できるかどうかで
確率の理解度が図れるかと思う。
続きを読む
夏休み。
私の会社は今日までで9連休。
自分の会社なので自分で休みを決めたのだけど、長かったな。
休みボケ。仕事モードになるのに時間がかかりそうだ・・。
今日は課題の5。確率を考えてみますか。

よくある間違いを2つ挙げました。
それぞれ明確な誤りの理由があって、指摘できるかどうかで
確率の理解度が図れるかと思う。
続きを読む
2023年07月08日
3連勝するには?
こんにちは。
7月。これから暑い夏・・
暑いのはあまり好きでない。
数学にノート整理など不要、と言う人はいるけど、
私はこういうルーズリーフにまとめていったものが、
何冊もありますね。

これを事あるごとに見返すと、記憶が定着します。
というか、見ないと忘れてしまうので。
今日は確率と数列の融合問題を1つ。

2人をA、Bとしていくつか求めてみます。

一般のnの場合、どうやって求めるのか?
場合の数を求めてnの式で表し、それを全事象の2のn乗で割ればいいけど、
では場合の数をどうやって求める?
漸化式をつくるよりない感じだけど、どう漸化式を作る?ここがムズいですね。
続きを読む
7月。これから暑い夏・・
暑いのはあまり好きでない。
数学にノート整理など不要、と言う人はいるけど、
私はこういうルーズリーフにまとめていったものが、
何冊もありますね。

これを事あるごとに見返すと、記憶が定着します。
というか、見ないと忘れてしまうので。
今日は確率と数列の融合問題を1つ。

2人をA、Bとしていくつか求めてみます。

一般のnの場合、どうやって求めるのか?
場合の数を求めてnの式で表し、それを全事象の2のn乗で割ればいいけど、
では場合の数をどうやって求める?
漸化式をつくるよりない感じだけど、どう漸化式を作る?ここがムズいですね。
続きを読む
2022年12月22日
期待値を求めるには?(その2)
こんにちは。
2022年もあとわずか。
近くのBarにて。
家で飲むのと同じものなのに、なんでうまいんだろ・・。

東京に単身上京、会社を経営して4年目の冬。
思ったより儲からないな、というのが本音だけど、
やりたい仕事ができていて、潰れることなく継続できている。
なので良しとせねば・・。と一人回想している。
期待値の問題。その2です。

全員が全くのランダムで名前を書くというのは現実ではあり得ないので、
この問題自体がナンセンスなのだけど、まぁそこは置いといて。
期待値=Σ(カップルの数)×(その確率)
なのだけど、確率を求めていくのが大変すぎですね。
なので何か工夫が必要です。ちょっとムズい。
続きを読む
2022年もあとわずか。
近くのBarにて。
家で飲むのと同じものなのに、なんでうまいんだろ・・。

東京に単身上京、会社を経営して4年目の冬。
思ったより儲からないな、というのが本音だけど、
やりたい仕事ができていて、潰れることなく継続できている。
なので良しとせねば・・。と一人回想している。
期待値の問題。その2です。

全員が全くのランダムで名前を書くというのは現実ではあり得ないので、
この問題自体がナンセンスなのだけど、まぁそこは置いといて。
期待値=Σ(カップルの数)×(その確率)
なのだけど、確率を求めていくのが大変すぎですね。
なので何か工夫が必要です。ちょっとムズい。
続きを読む
2022年12月14日
期待値を求めるには?(その1)
こんにちは。
今年も残り半月ですか、早いものだなと、毎年言ってるような・・。
高校の確率の話。

写真のさいころは六面体でなくて、十面体と十二面体です。
十面体の方は、
0、1、2、3、4、5、6、7、8、9
の目があるけど、0を10とします。
すると、1回の出る目の期待値は5.5になる。
十面体を3回まで投げていいことにして、なるべく高い数を出したい
という場合、1、2回目でやめるかどうかの判断をどうすればよいか?
これを考えてみました。

さいころは、どの目が出るのも等しい確率とします。
3回だとムズいので、2回だけ投げる場合を考えると、
5が出た場合、期待値の5.5より低いので、当然次を投げる。
6が出た場合、期待値の5.5より高いので、ここでやめた方がいい。
つまり、
現在の得点>次に得られる数の期待値 なら、ここでやめる
現在の得点<次に得られる数の期待値 なら、次を振る
という基準で行きます。
この問題は3回チャレンジできるので、1回目から2回目に行く基準が、
2回目から3回目に行く基準よりもゆるくなりますね。このあたりが難しい。
続きを読む
今年も残り半月ですか、早いものだなと、毎年言ってるような・・。
高校の確率の話。

写真のさいころは六面体でなくて、十面体と十二面体です。
十面体の方は、
0、1、2、3、4、5、6、7、8、9
の目があるけど、0を10とします。
すると、1回の出る目の期待値は5.5になる。
十面体を3回まで投げていいことにして、なるべく高い数を出したい
という場合、1、2回目でやめるかどうかの判断をどうすればよいか?
これを考えてみました。

さいころは、どの目が出るのも等しい確率とします。
3回だとムズいので、2回だけ投げる場合を考えると、
5が出た場合、期待値の5.5より低いので、当然次を投げる。
6が出た場合、期待値の5.5より高いので、ここでやめた方がいい。
つまり、
現在の得点>次に得られる数の期待値 なら、ここでやめる
現在の得点<次に得られる数の期待値 なら、次を振る
という基準で行きます。
この問題は3回チャレンジできるので、1回目から2回目に行く基準が、
2回目から3回目に行く基準よりもゆるくなりますね。このあたりが難しい。
続きを読む
2022年05月08日
座れる確率は?
こんにちは。
GWも今日で終わりか・・。

岐阜県にある合掌村というところ。
昔々の合掌造りという家を復元した建物があって、
なかなか興味深かった。
本日電車で東京に戻るのだけど、
座席は座れそうです。よかった。
で、座席の問を1つ。

何となく五分五分?
席を少なくして計算してみると、大体1/2になります。
ほんとに1/2かどうか?
これは漸化式を作るしかないかな・・。
続きを読む
GWも今日で終わりか・・。

岐阜県にある合掌村というところ。
昔々の合掌造りという家を復元した建物があって、
なかなか興味深かった。
本日電車で東京に戻るのだけど、
座席は座れそうです。よかった。
で、座席の問を1つ。

何となく五分五分?
席を少なくして計算してみると、大体1/2になります。
ほんとに1/2かどうか?
これは漸化式を作るしかないかな・・。
続きを読む
2022年01月15日
玉を取り出す確率は?
こんにちは。
大学入試の共通テストがいよいよ明日か。
もうすでに受験勉強は完璧に終わった!
という受験生、なかなかいないでしょうね。不安はつきもの。
去年の共通テスト数学1Aと2B、解いてみて感じたことは、
何だろ・・
文章が多くて解くのがメンドウ、しかも問がつまらん。
こんなところ。しかしそんなこと言っても解かなくては合格しない。
共通テスト数学の特徴。真面目に書くと、こうかな・・。
1)日常の題材に無理やり結び付けて、数学が役に立つ感を見せた
2)対話文や答の選択式といった国語のような体裁で新傾向感を出した
3)文章を長くし過程を重視したように見せているが、要は時間攻めが狙い
今年はどうだろう・・?
今日は確率の問題を1つ。
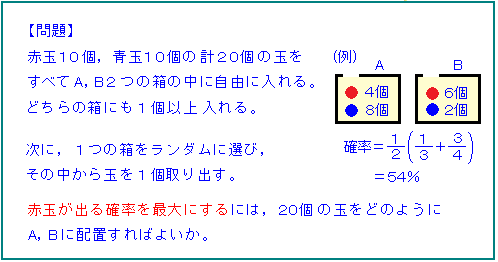
半々に分けた場合は当然確率50%で、
A、Bの比率を変えて計算してみると、確率が上がるようです。
これをきちんと説明するのは、簡単でないですね。
文字をいくつか置いてみて、関数っぽく解くしかない。
続きを読む
大学入試の共通テストがいよいよ明日か。
もうすでに受験勉強は完璧に終わった!
という受験生、なかなかいないでしょうね。不安はつきもの。
去年の共通テスト数学1Aと2B、解いてみて感じたことは、
何だろ・・
文章が多くて解くのがメンドウ、しかも問がつまらん。
こんなところ。しかしそんなこと言っても解かなくては合格しない。
共通テスト数学の特徴。真面目に書くと、こうかな・・。
1)日常の題材に無理やり結び付けて、数学が役に立つ感を見せた
2)対話文や答の選択式といった国語のような体裁で新傾向感を出した
3)文章を長くし過程を重視したように見せているが、要は時間攻めが狙い
今年はどうだろう・・?
今日は確率の問題を1つ。

半々に分けた場合は当然確率50%で、
A、Bの比率を変えて計算してみると、確率が上がるようです。
これをきちんと説明するのは、簡単でないですね。
文字をいくつか置いてみて、関数っぽく解くしかない。
続きを読む
2021年10月28日
全曲再生するには?
こんにちは。
ふう、しばし休憩。

音楽を聴く方法が時代とともに変わってきていて、
今はほんとに便利になったなと思う。
ずいぶん前の写真を探してきたのだけど・・

当時ドーナツ盤と呼ばれていた。
家にまだあるかな・・。
音楽を聴く問を1つ。

ランダム再生は、毎回、100曲のうちのどれかが等しい確率で再生されることとします。
ずいぶん前に解いたのだけど、こちら
これとは違う解き方を発見したので、UPします。
続きを読む
ふう、しばし休憩。

音楽を聴く方法が時代とともに変わってきていて、
今はほんとに便利になったなと思う。
ずいぶん前の写真を探してきたのだけど・・

当時ドーナツ盤と呼ばれていた。
家にまだあるかな・・。
音楽を聴く問を1つ。

ランダム再生は、毎回、100曲のうちのどれかが等しい確率で再生されることとします。
ずいぶん前に解いたのだけど、こちら
これとは違う解き方を発見したので、UPします。
続きを読む
2021年10月11日
カタラン数とは?
こんにちは。
新車がやっと届きました。

3月に契約をして、なんだかんだと納車が遅れてやっとです。
人気があるのだとか。最近の車は、乗り心地抜群なのだけど、
ほんとにメカニズムというか、いろんな装置があってわからぬ・・。
数学の話。
カタラン数というのはこちら。
今日はこれを考えてみますか?

この答えが「カタラン数」になるとのことです。
玉を入れていく途中で、白玉の方が多くなってはダメというルールです。
全パターンを書き出していけばわかるのだけど、何かうまい求め方はないか?
1つは、赤玉をa、白玉をbとして取り出した順に左から並べていく。例えば
aababbaab
という10個の順列は、左から見ていくと、いつでも
aの個数≧bの個数
になっているので条件に合う順列となります。
なのでこういう並び方の総数を求めればいい。けど、どうやって計算式をつくるのか?
別の考え方で、次の図。

1回目は必ず赤で、最後は必ず白になります。その間は、
入れる玉の色と図の進む方向を対応させることにすると、場合の数は
上の図の道順の総数に等しくなります。
これはいろんなサイトに載っている方法です。
赤5個、白5個なら数えていけばわかるけど、
赤n個、白n個の一般式を求める場合、どうすればよいだろう?
続きを読む
新車がやっと届きました。

3月に契約をして、なんだかんだと納車が遅れてやっとです。
人気があるのだとか。最近の車は、乗り心地抜群なのだけど、
ほんとにメカニズムというか、いろんな装置があってわからぬ・・。
数学の話。
カタラン数というのはこちら。
今日はこれを考えてみますか?

この答えが「カタラン数」になるとのことです。
玉を入れていく途中で、白玉の方が多くなってはダメというルールです。
全パターンを書き出していけばわかるのだけど、何かうまい求め方はないか?
1つは、赤玉をa、白玉をbとして取り出した順に左から並べていく。例えば
aababbaab
という10個の順列は、左から見ていくと、いつでも
aの個数≧bの個数
になっているので条件に合う順列となります。
なのでこういう並び方の総数を求めればいい。けど、どうやって計算式をつくるのか?
別の考え方で、次の図。

1回目は必ず赤で、最後は必ず白になります。その間は、
入れる玉の色と図の進む方向を対応させることにすると、場合の数は
上の図の道順の総数に等しくなります。
これはいろんなサイトに載っている方法です。
赤5個、白5個なら数えていけばわかるけど、
赤n個、白n個の一般式を求める場合、どうすればよいだろう?
続きを読む
2021年09月09日
条件付き確率の問
こんにちは。
調律。久々です。

鍵盤を押すと、ハンマーが弦を打つことで音が鳴ります。
しかしこれだけではごく小さな音なのだけど、空気を振動させるものが
中にあるので、これによって大きな音になります。
素晴らしい楽器だと思う。良い音を出す腕は無いけど・・。
数学の話。
「条件付き確率」というのは、高校の数学Aで習う。問題文の中に、
●●が起こったときの〇〇が起こる確率
と書いてあれば、大体それです。
似ているようで違う条件付き確率の問を2つほど。

「子どもの中に女の子がいる」
と言う条件のもとで、2人とも女の子である確率を求める問題。
次は少し場面が違います。

「子どもの中に女の子がいる」
と言う条件は同じなのだけど、実際に1人が現れている。
この状況で、問1と確率が異なるのかどうか?
どうでしょう・・?
同じように見えるし、違うようにも思える・・。
続きを読む
調律。久々です。

鍵盤を押すと、ハンマーが弦を打つことで音が鳴ります。
しかしこれだけではごく小さな音なのだけど、空気を振動させるものが
中にあるので、これによって大きな音になります。
素晴らしい楽器だと思う。良い音を出す腕は無いけど・・。
数学の話。
「条件付き確率」というのは、高校の数学Aで習う。問題文の中に、
●●が起こったときの〇〇が起こる確率
と書いてあれば、大体それです。
似ているようで違う条件付き確率の問を2つほど。

「子どもの中に女の子がいる」
と言う条件のもとで、2人とも女の子である確率を求める問題。
次は少し場面が違います。

「子どもの中に女の子がいる」
と言う条件は同じなのだけど、実際に1人が現れている。
この状況で、問1と確率が異なるのかどうか?
どうでしょう・・?
同じように見えるし、違うようにも思える・・。
続きを読む
2020年10月06日
原因の確率とは?
こんにちは
もう10月ですか、早いですね。
東京に越して、1年半ほど経ちました。

通勤の電車は一時期すいていたけど、最近は元に戻って混んでいる。
東京に来て何を買ったかといえば、ノートカバー。
これがあるとどこでも仕事がしやすい。
田舎にいるときは考えもしなかったな・・。
数学の話。
「原因の確率って何ですか?」
という問い合わせがありました。
・取り出した玉が赤玉だったとき、それが袋Aのものである確率
・検査をして陽性と判定されたとき、ほんとは陰性である確率
こういう感じの、条件付き確率のことです。
実生活にありそうな問題を1つ。

居酒屋で忘れる確率が40%というのは、カサを置いて酒を飲むと、
10回に4回はカサを忘れてきてしまう、という感じです。
しかしこの場合、コンビニ、図書館と立ち寄っているので、そのまま40%にはなりません。
3か所それぞれで忘れる確率を計算して、
最も確率の高いところに取りに帰る
という方針になるかな。
続きを読む
もう10月ですか、早いですね。
東京に越して、1年半ほど経ちました。

通勤の電車は一時期すいていたけど、最近は元に戻って混んでいる。
東京に来て何を買ったかといえば、ノートカバー。
これがあるとどこでも仕事がしやすい。
田舎にいるときは考えもしなかったな・・。
数学の話。
「原因の確率って何ですか?」
という問い合わせがありました。
・取り出した玉が赤玉だったとき、それが袋Aのものである確率
・検査をして陽性と判定されたとき、ほんとは陰性である確率
こういう感じの、条件付き確率のことです。
実生活にありそうな問題を1つ。

居酒屋で忘れる確率が40%というのは、カサを置いて酒を飲むと、
10回に4回はカサを忘れてきてしまう、という感じです。
しかしこの場合、コンビニ、図書館と立ち寄っているので、そのまま40%にはなりません。
3か所それぞれで忘れる確率を計算して、
最も確率の高いところに取りに帰る
という方針になるかな。
続きを読む
2019年11月05日
スパゲティ問題(その2)
こんにちは。
11月に入った。東京も寒いですね。
東京で会社を経営するハメになり、半年が過ぎた。
幸い、私に仕事を頼みたいと言う人が少数いらして、
何とかやって行けてるところかな。
まあ来年はわかりませんが・・。
昨日の続きの確率です。

(2)で、はじめに2つに分けたとき、偶然同じ長さになった場合は、
どちらか一方を2つに分けるものとします。
(1)と(2)の確率は同じではなかろーか?
はじめそう思ったけど、大間違いでした。

今度は、xを決めたあとに確率を考えることになるので、
確率がxの関数で表されることになります。
ここが(1)とは違うところです。
続きを読む
11月に入った。東京も寒いですね。
東京で会社を経営するハメになり、半年が過ぎた。
幸い、私に仕事を頼みたいと言う人が少数いらして、
何とかやって行けてるところかな。
まあ来年はわかりませんが・・。
昨日の続きの確率です。

(2)で、はじめに2つに分けたとき、偶然同じ長さになった場合は、
どちらか一方を2つに分けるものとします。
(1)と(2)の確率は同じではなかろーか?
はじめそう思ったけど、大間違いでした。

今度は、xを決めたあとに確率を考えることになるので、
確率がxの関数で表されることになります。
ここが(1)とは違うところです。
続きを読む
2019年11月03日
スパゲティ問題(その1)
こんにちは。
東京新宿、とある珈琲店にて。

東京に越してきて半年、珈琲店巡りをしているのだけど、
ここが一番うまいです。コクと香り、苦みの中に甘みがある。
しかし珈琲1杯で1人で粘る客は、悪い客。
次の問題に悩んでおりました。

「スパゲティ問題」で検索すると、いろいろ出てきます。
高校までの数学だと、場合の数を使うものしかやらない(数Bで確率変数は習うけど)
ので、この確率は高校の範囲外です。
例えば、下の正方形の内部に無作為に1点Pをとるとき,黄色の三角形の中にPがある確率は?

これは面積の比率を考えて、1/4となります。
こんな感じで(1)を解きます。
(1)も(2)も確率は同じだと思っていたけど、違うようです。
今日は(1)のみで。
続きを読む
東京新宿、とある珈琲店にて。

東京に越してきて半年、珈琲店巡りをしているのだけど、
ここが一番うまいです。コクと香り、苦みの中に甘みがある。
しかし珈琲1杯で1人で粘る客は、悪い客。
次の問題に悩んでおりました。

「スパゲティ問題」で検索すると、いろいろ出てきます。
高校までの数学だと、場合の数を使うものしかやらない(数Bで確率変数は習うけど)
ので、この確率は高校の範囲外です。
例えば、下の正方形の内部に無作為に1点Pをとるとき,黄色の三角形の中にPがある確率は?

これは面積の比率を考えて、1/4となります。
こんな感じで(1)を解きます。
(1)も(2)も確率は同じだと思っていたけど、違うようです。
今日は(1)のみで。
続きを読む
2018年06月04日
条件付き確率。
こんにちは。
多忙の為、更新できず・・。
模試を作問していて、ずっと行き詰っていた。
条件付き確率
これは高校の数学Aで習うのだけど、何か条件が設定されたときに
ある事柄が起こる確率のことです。作問をする側から言うと、
条件を付けること自体が不自然になってしまうことが多々あって、
何だか作りにくい。
条件付きが不自然でなく、ちょっと面白い問を見つけた。

どこかの大学入試問題を短くアレンジしました。
「この人は空腹に耐えかねた」
という文面があったので、仕方ない状況だったのでしょう。

XがA~Dのどれになるかで、この4パターンがありますが、
④はDがXなので、カラスがDを食べることはないです。
比較することは、次の2つの大小です。
カラスがDを食べたという条件のもとで、
・AがXである確率
・BがXである確率
もともと、AがXである確率もBがXである確率も同じ1/4ですが、
「カラスがDを食べた」という条件を付けると、確率が変わってしまう
可能性があり、そのことを考慮する必要があります。
ここがヒジョーにややこしい。
続きを読む
多忙の為、更新できず・・。
模試を作問していて、ずっと行き詰っていた。
条件付き確率
これは高校の数学Aで習うのだけど、何か条件が設定されたときに
ある事柄が起こる確率のことです。作問をする側から言うと、
条件を付けること自体が不自然になってしまうことが多々あって、
何だか作りにくい。
条件付きが不自然でなく、ちょっと面白い問を見つけた。

どこかの大学入試問題を短くアレンジしました。
「この人は空腹に耐えかねた」
という文面があったので、仕方ない状況だったのでしょう。

XがA~Dのどれになるかで、この4パターンがありますが、
④はDがXなので、カラスがDを食べることはないです。
比較することは、次の2つの大小です。
カラスがDを食べたという条件のもとで、
・AがXである確率
・BがXである確率
もともと、AがXである確率もBがXである確率も同じ1/4ですが、
「カラスがDを食べた」という条件を付けると、確率が変わってしまう
可能性があり、そのことを考慮する必要があります。
ここがヒジョーにややこしい。
続きを読む
2018年02月07日
大学受験対策(場合の数)
こんにちは。
樹形図の授業中・・。

数学が嫌いで苦手な高1生たち。3桁の整数の樹形図に悪戦苦闘で、
「2が2つあるのに、樹形図ではなぜ1個しか書かない?」
と聞いてくる。意味がわからなかった、この質問・・。
算数でつまずいてからずっとわからないで来た、と言うけど、どうもそれ以前の
問題かもしれない。数をかぞえるとかお金を計算するとか、身近なところで数に
接することが少なかったか、考えずに今まで過ごしてきたか・・。
なら、数に接する機会を多く取らねば。
前途多難がまだまだ続く・・。
私立大の入試がちらほら始まってますね。
場合の数を求める問題を3題ほど。

<目安>
1問正解・・・偏差値45
2問正解・・・偏差値50
3問正解・・・偏差値55
(3)は余事象だと面倒なので、nCr一発で求めたい。
続きを読む
樹形図の授業中・・。

数学が嫌いで苦手な高1生たち。3桁の整数の樹形図に悪戦苦闘で、
「2が2つあるのに、樹形図ではなぜ1個しか書かない?」
と聞いてくる。意味がわからなかった、この質問・・。
算数でつまずいてからずっとわからないで来た、と言うけど、どうもそれ以前の
問題かもしれない。数をかぞえるとかお金を計算するとか、身近なところで数に
接することが少なかったか、考えずに今まで過ごしてきたか・・。
なら、数に接する機会を多く取らねば。
前途多難がまだまだ続く・・。
私立大の入試がちらほら始まってますね。
場合の数を求める問題を3題ほど。

<目安>
1問正解・・・偏差値45
2問正解・・・偏差値50
3問正解・・・偏差値55
(3)は余事象だと面倒なので、nCr一発で求めたい。
続きを読む
2016年12月06日
結婚問題(秘書問題)
こんにちは。
結婚相手を見つけるのに、何人目でOKするのが数学的に最良か?
次は、「結婚問題」とか「秘書問題」またはナンパ問題とか呼ばれる確率の問題です。

補足すると、
見合いは無作為な順序で1人ずつ行い、見合いの時以外で男性と会うことは無い。
男性100人にはユキの好みの順に1位から100位までの順位をつけることができて、
ユキはその順位に基づいて決定を行う。
以前、「林先生が驚く初耳学」と言う番組で解説されていたのだけど、これを解くのは難しい。
10人だけにして、初めの4人を見送る場合を考えてみると、
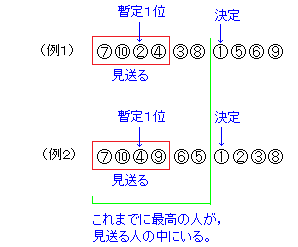
このように、
第1位の人より前の人の中での暫定1位が、見送る4人の中にいる
というのが条件となる。
続きを読む
結婚相手を見つけるのに、何人目でOKするのが数学的に最良か?
次は、「結婚問題」とか「秘書問題」またはナンパ問題とか呼ばれる確率の問題です。

補足すると、
見合いは無作為な順序で1人ずつ行い、見合いの時以外で男性と会うことは無い。
男性100人にはユキの好みの順に1位から100位までの順位をつけることができて、
ユキはその順位に基づいて決定を行う。
以前、「林先生が驚く初耳学」と言う番組で解説されていたのだけど、これを解くのは難しい。
10人だけにして、初めの4人を見送る場合を考えてみると、

このように、
第1位の人より前の人の中での暫定1位が、見送る4人の中にいる
というのが条件となる。
続きを読む
2016年10月06日
ポリアの壺
こんにちは。
土日、四国へ行って来ました。
長野⇒東京羽田⇒松山という飛行機の旅。

いま雲の上を飛んでいる。外を見ると足がすくむ・・。
「いかにして問題を解くか」
この著者ジョージポリアという人の本を読んでいたところ、
コーヒーの機内サービスが来た。
次は「ポリアの壺」という有名な確率の問題。

玉が1個ずつ増えていくので、すべての場合を描いていくとえらいことになる。
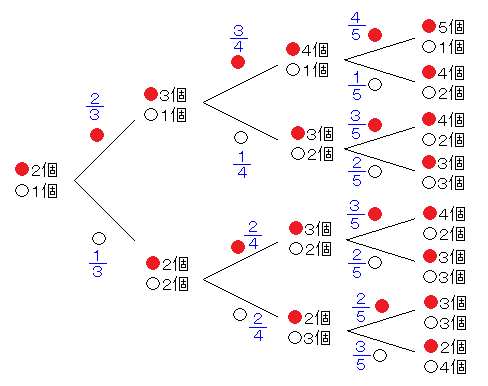
確率を掛け合わせて排反なものを足していくという方法では無理ですね。
こういう場合は、漸化式を立てるのが1つの手です。しかし立て方がムズい・・。
続きを読む
土日、四国へ行って来ました。
長野⇒東京羽田⇒松山という飛行機の旅。

いま雲の上を飛んでいる。外を見ると足がすくむ・・。
「いかにして問題を解くか」
この著者ジョージポリアという人の本を読んでいたところ、
コーヒーの機内サービスが来た。
次は「ポリアの壺」という有名な確率の問題。

玉が1個ずつ増えていくので、すべての場合を描いていくとえらいことになる。

確率を掛け合わせて排反なものを足していくという方法では無理ですね。
こういう場合は、漸化式を立てるのが1つの手です。しかし立て方がムズい・・。
続きを読む
2016年08月27日
バスの待ち時間。
こんにちは。
市内の学校は夏休みがすでに終わっていて、今週から2学期が始まっている。
塾の授業にて。
休みが明け、三角関数の公式などすべて忘れてしまった生徒がいた。
あまりに不出来なので、徐々に私は機嫌が悪くなっていった・・。

例によって、大事なことを紙に書いてあげ、こう言った。
「家のトイレに貼っておけ!!」
勉強で大事なことは、今日やったことを明日も見返すこと。
これをやらないもんだから、数学が一向に上達しない・・。
前回の続きで、待ち時間の平均を求める問題。

先週からずっと考えていた・・。
前回のケンとユキの待ち時間の結果を使って解く感じだけど、かなり難。
続きを読む
市内の学校は夏休みがすでに終わっていて、今週から2学期が始まっている。
塾の授業にて。
休みが明け、三角関数の公式などすべて忘れてしまった生徒がいた。
あまりに不出来なので、徐々に私は機嫌が悪くなっていった・・。

例によって、大事なことを紙に書いてあげ、こう言った。
「家のトイレに貼っておけ!!」
勉強で大事なことは、今日やったことを明日も見返すこと。
これをやらないもんだから、数学が一向に上達しない・・。
前回の続きで、待ち時間の平均を求める問題。

先週からずっと考えていた・・。
前回のケンとユキの待ち時間の結果を使って解く感じだけど、かなり難。
続きを読む





