2024年08月04日
夏休み課題その3
こんにちは。
これは私の数学ノートで、ルーズリーフで分野ごとにまとめてます。
若い頃からの蓄積でもう10冊ほどになりますね。

数学にノート整理など不要!と言う人いるけど、人は覚えたことを
忘れる生き物です。このノートを毎日見返して記憶を定着させます。
赤青2色使って、見やすくするとなお覚えやすい。ぜひお試しを。
今日は課題のその3です。

この不等式を私はアーノルドと呼んでいました。シュワルツの親戚ということで・・。
(ア)はどの参考書にも載っているちょっとうまい方法です。
(イ)は2次関数のグラフを考える方法で、(ウ)は内積です。
この証明法を(ア)しか知らない人は、これを機に全部知っておいてほしい。
きっと学力の幅がやや広がることと思う。
続きを読む
これは私の数学ノートで、ルーズリーフで分野ごとにまとめてます。
若い頃からの蓄積でもう10冊ほどになりますね。

数学にノート整理など不要!と言う人いるけど、人は覚えたことを
忘れる生き物です。このノートを毎日見返して記憶を定着させます。
赤青2色使って、見やすくするとなお覚えやすい。ぜひお試しを。
今日は課題のその3です。

この不等式を私はアーノルドと呼んでいました。シュワルツの親戚ということで・・。
(ア)はどの参考書にも載っているちょっとうまい方法です。
(イ)は2次関数のグラフを考える方法で、(ウ)は内積です。
この証明法を(ア)しか知らない人は、これを機に全部知っておいてほしい。
きっと学力の幅がやや広がることと思う。
続きを読む
2024年08月01日
夏休み課題その2
こんにちは。
もう7月も終わりですか。
中高生はもう夏休みに入っていると思う。

長い休みには、こういう分厚い参考書を端からやっていく。
という学習法は力をつけるのに良いかと思う。しかし、
1)予定通り進まず中途半端で終わる
2)学習したことを端から忘れていく
ということが起こりがちですね。
ではどうすればいいか?思うことを記事の最後に書いておきます。
今日は課題のその2です。

(ア)はどの参考書にも載っているけど、(イ)(ウ)は分野が違うから
なかなか無いでしょう。でもこういう考え方ができると学力の幅が広がる。
続きを読む
もう7月も終わりですか。
中高生はもう夏休みに入っていると思う。

長い休みには、こういう分厚い参考書を端からやっていく。
という学習法は力をつけるのに良いかと思う。しかし、
1)予定通り進まず中途半端で終わる
2)学習したことを端から忘れていく
ということが起こりがちですね。
ではどうすればいいか?思うことを記事の最後に書いておきます。
今日は課題のその2です。

(ア)はどの参考書にも載っているけど、(イ)(ウ)は分野が違うから
なかなか無いでしょう。でもこういう考え方ができると学力の幅が広がる。
続きを読む
2024年07月29日
夏休み課題その1
こんにちは。
ずいぶんと更新ができずにいて、気がつけばもう8月ですね・・。
この半年ただただ多忙過ぎて手が回らなかった。それだけです。
このblogは、塾の講師をしていたとき、中高生に数学に興味を持ってもらえる
ようにと始めたもので、2008年開設だからもうかれこれ16年になりますね。
今は先生ではなく小さな会社の社長だけど、思う気持ちは16年前と変わらない。
数学は面白い学問。
ぜひその面白さを見つけて楽しんでほしい、と願う。
大学入試を目指す受験生に有益な数学の問をいくつか作りました。
今日はその1です。

2変数の最大・最小問題のうち、条件が2次式で求める値が1次式の場合です。
1次式=kとおいてxかyを消去し、判別式≧0とする
のが基本的な解法でしょうけど、条件式が円の場合はいろいろ手があって、
これ以外の解法を考えてみてください。
続きを読む
ずいぶんと更新ができずにいて、気がつけばもう8月ですね・・。
この半年ただただ多忙過ぎて手が回らなかった。それだけです。
このblogは、塾の講師をしていたとき、中高生に数学に興味を持ってもらえる
ようにと始めたもので、2008年開設だからもうかれこれ16年になりますね。
今は先生ではなく小さな会社の社長だけど、思う気持ちは16年前と変わらない。
数学は面白い学問。
ぜひその面白さを見つけて楽しんでほしい、と願う。
大学入試を目指す受験生に有益な数学の問をいくつか作りました。
今日はその1です。

2変数の最大・最小問題のうち、条件が2次式で求める値が1次式の場合です。
1次式=kとおいてxかyを消去し、判別式≧0とする
のが基本的な解法でしょうけど、条件式が円の場合はいろいろ手があって、
これ以外の解法を考えてみてください。
続きを読む
2023年08月13日
円と直線の交点の座標は?
こんにちは。
お盆のさなか、今日は久々のオフです。
数学の話。
円と直線の交点の座標を求めるとき、例えば次。

これは次のように結構面倒な計算になる。

他に手がないかどうか、考えてみました。

円を①、直線を②として、次の順。
Step1 ②をxかyについて解いて、それを①に代入
Step2 2次方程式を作って解の公式にぶち込む。
Step3 求めた値を②に代入し、もう一方を出す。
この問は係数が文字なので相当大変だけど、
受験生は1回は解いてみると何か得るものがあるかと思う。
しかし今日はこれではない解法で。
続きを読む
お盆のさなか、今日は久々のオフです。
数学の話。
円と直線の交点の座標を求めるとき、例えば次。

これは次のように結構面倒な計算になる。

他に手がないかどうか、考えてみました。

円を①、直線を②として、次の順。
Step1 ②をxかyについて解いて、それを①に代入
Step2 2次方程式を作って解の公式にぶち込む。
Step3 求めた値を②に代入し、もう一方を出す。
この問は係数が文字なので相当大変だけど、
受験生は1回は解いてみると何か得るものがあるかと思う。
しかし今日はこれではない解法で。
続きを読む
2023年06月28日
レムニスケートとは?
こんにちは。
東京は銀座、和食の店にて。

折角なのでと高級な店を予約した。
うまかったな~~。高かったけど・・。
数学の話。
レムニスケートというものがあります。
youtubeのとある数学のサイトで紹介されていた問題。

この曲線は、次のようになります。

極座標と言って、
x=rcosθ,y=rsinθ
とおくと、きれいな式になる場合があり、この問もその例です。
続きを読む
東京は銀座、和食の店にて。

折角なのでと高級な店を予約した。
うまかったな~~。高かったけど・・。
数学の話。
レムニスケートというものがあります。
youtubeのとある数学のサイトで紹介されていた問題。

この曲線は、次のようになります。

極座標と言って、
x=rcosθ,y=rsinθ
とおくと、きれいな式になる場合があり、この問もその例です。
続きを読む
2023年05月29日
連立方程式と算術。
こんにちは。
ツアーオブジャパンという自転車のレースがありました。こちら。
信州飯田コース。毎年我が家の前を、こういう感じで走ります。

我が家に近所の人や親せきが集まって観戦したとのこと。
私は東京で仕事でしたが・・。
中学2年の連立方程式の問題。

求めたいものをxやyとおいて、式を作ると、

こうなるので、これを解けばOK。
今日はこれで終わりでなく、算数で解く方法を考えてみました。
【つるかめ算】
ツルとカメの全体の数と、足の合計がわかっているとき、それぞれの数を求めるときに使う解法。
その方法は、まず全部がツルだったとして足の合計本数の違いを求め、
(合計本数の違い)÷(1匹の本数の違い)から、カメの数が出る。そしてツルの数も出る。
というものです。この方法で解くと、こうなります。
全体を時速30kmで走ったとすると、進んだ道のりは、10km
これだと2km足りないので、時速を50kmに変えていく。
1時間あたり20km道のりが変わるから、2kmだけ変えるには、
2÷20=0.1(時間)
これが時速50kmで走る時間になる。
よって、くだりの道のりは、50×0.1=5km
(答) のぼり 7km
わかりにくいですね。どれがツルで、どれがカメか?
これを中学受験の小学生に教えることが、実に難しい。
もう少しわかりやすい方法で。
続きを読む
ツアーオブジャパンという自転車のレースがありました。こちら。
信州飯田コース。毎年我が家の前を、こういう感じで走ります。

我が家に近所の人や親せきが集まって観戦したとのこと。
私は東京で仕事でしたが・・。
中学2年の連立方程式の問題。

求めたいものをxやyとおいて、式を作ると、

こうなるので、これを解けばOK。
今日はこれで終わりでなく、算数で解く方法を考えてみました。
【つるかめ算】
ツルとカメの全体の数と、足の合計がわかっているとき、それぞれの数を求めるときに使う解法。
その方法は、まず全部がツルだったとして足の合計本数の違いを求め、
(合計本数の違い)÷(1匹の本数の違い)から、カメの数が出る。そしてツルの数も出る。
というものです。この方法で解くと、こうなります。
全体を時速30kmで走ったとすると、進んだ道のりは、10km
これだと2km足りないので、時速を50kmに変えていく。
1時間あたり20km道のりが変わるから、2kmだけ変えるには、
2÷20=0.1(時間)
これが時速50kmで走る時間になる。
よって、くだりの道のりは、50×0.1=5km
(答) のぼり 7km
わかりにくいですね。どれがツルで、どれがカメか?
これを中学受験の小学生に教えることが、実に難しい。
もう少しわかりやすい方法で。
続きを読む
2023年05月12日
3変数の関数のばあい。
こんにちは。
GWがあっという間に終わり、またいつもの日常です。

三石家恒例のGW-BBQ大会。家の庭にて。
ホタテにはバターが合う。シイタケは自家製。
大勢でワイワイやるのが良いですね。
今週、こんな問を考えておりました。

(a,b,c)=(0,0,1)のとき、T=0
(a,b,c)=(1/3,1/3,1/3)のとき、T=1/3
これらが最小値と最大値になりそうだけど、
この2つの値の間をすべて取るかはわからない。
ちなみに最大値だけを出すなら、次の手がある。

文字が多い場合、
どれか1つを固定する
という考え方が結構役に立ちます。
続きを読む
GWがあっという間に終わり、またいつもの日常です。

三石家恒例のGW-BBQ大会。家の庭にて。
ホタテにはバターが合う。シイタケは自家製。
大勢でワイワイやるのが良いですね。
今週、こんな問を考えておりました。

(a,b,c)=(0,0,1)のとき、T=0
(a,b,c)=(1/3,1/3,1/3)のとき、T=1/3
これらが最小値と最大値になりそうだけど、
この2つの値の間をすべて取るかはわからない。
ちなみに最大値だけを出すなら、次の手がある。

文字が多い場合、
どれか1つを固定する
という考え方が結構役に立ちます。
続きを読む
2023年01月14日
正弦定理と余弦定理
こんにちは。
大学入学共通テスト、1日目が終わりましたね。
数学は明日ですか。
どこかネットで問題がUPされ次第、解いてみます。
ところで試験中、問が解けないときどうすればいいか?

まあ、普通に考えて解けないのだから、見落としを見つけるか、
何か特別なことを見つけるか、ということでこの4つかなと思う。
数学Ⅰの「図形と計量」という分野に正弦定理、余弦定理があるけど、
これの成り立ちを問う問題が、以前の試行テストで出ましたね。
定理が成り立つ理由、というのもある程度押さえておくべきです。

pは正弦定理のようなもの
qは余弦定理のようなもの
です。
どちらも三角形ABCが出てきていないので、変な問いですね。
pとqが同値であることを示すには、
p ⇒ q
q ⇒ p
がともに真であることを示します。
続きを読む
大学入学共通テスト、1日目が終わりましたね。
数学は明日ですか。
どこかネットで問題がUPされ次第、解いてみます。
ところで試験中、問が解けないときどうすればいいか?

まあ、普通に考えて解けないのだから、見落としを見つけるか、
何か特別なことを見つけるか、ということでこの4つかなと思う。
数学Ⅰの「図形と計量」という分野に正弦定理、余弦定理があるけど、
これの成り立ちを問う問題が、以前の試行テストで出ましたね。
定理が成り立つ理由、というのもある程度押さえておくべきです。

pは正弦定理のようなもの
qは余弦定理のようなもの
です。
どちらも三角形ABCが出てきていないので、変な問いですね。
pとqが同値であることを示すには、
p ⇒ q
q ⇒ p
がともに真であることを示します。
続きを読む
2022年11月12日
相加・相乗平均の誤答多い。
こんにちは。
久々の休日。
良い音楽を聴きながら、コーヒーでも飲みますか。

「ネル」というパジャマの生地でできたコーヒーを濾す道具です。
これで淹れると、角が取れてまろやかな味になる。
気がする・・。
今日はこういう問を1つ。

この問題にはいろいろと誤答がありますね。
塾で教えていた頃に、生徒に誤答例を見せてどこが間違いか?
考えてもらったことがあります。
では1つ目の誤答です。

見た感じ正しいように見えるけど、大間違いです。
生徒A:「赤い枠の中の不等式が、そもそも間違っているのでは?」
生徒B:「作った不等式の右辺が定数にならないから、ダメなんじゃ?」
では2つ目の誤答です。

これも、一見うまそうに見えますね。でも間違いです。
生徒C:「今度は合っていると思う。」
生徒D:「①と②を掛け合わせてはいけないのでは?」
掛け合わせること自体は間違いではなく、正しい不等式が出てきてます。
誤答2は等号が成り立つ場合が、実はない。なので8を最小値にできないのです。
続きを読む
久々の休日。
良い音楽を聴きながら、コーヒーでも飲みますか。

「ネル」というパジャマの生地でできたコーヒーを濾す道具です。
これで淹れると、角が取れてまろやかな味になる。
気がする・・。
今日はこういう問を1つ。

この問題にはいろいろと誤答がありますね。
塾で教えていた頃に、生徒に誤答例を見せてどこが間違いか?
考えてもらったことがあります。
では1つ目の誤答です。

見た感じ正しいように見えるけど、大間違いです。
生徒A:「赤い枠の中の不等式が、そもそも間違っているのでは?」
生徒B:「作った不等式の右辺が定数にならないから、ダメなんじゃ?」
では2つ目の誤答です。

これも、一見うまそうに見えますね。でも間違いです。
生徒C:「今度は合っていると思う。」
生徒D:「①と②を掛け合わせてはいけないのでは?」
掛け合わせること自体は間違いではなく、正しい不等式が出てきてます。
誤答2は等号が成り立つ場合が、実はない。なので8を最小値にできないのです。
続きを読む
2022年11月04日
続、複素数平面に強くなるには?
こんにちは。
高校数学Ⅲの「複素数平面」という分野の原稿を書いていて、
何とかすべて書き終えました。ふう・・。

この汚ない原稿は私が書いたもので、これを組版すると、
こうなる。

この瞬間が、この仕事のちょっと嬉しいときですね。
中高生にとって、もっともっと役に立つ良い本を作りたい。
こういう気持ちで仕事をしている。
あれれ・・この中に誤植がある・・。
今日はこういう、教科書にありそな問を1つ。
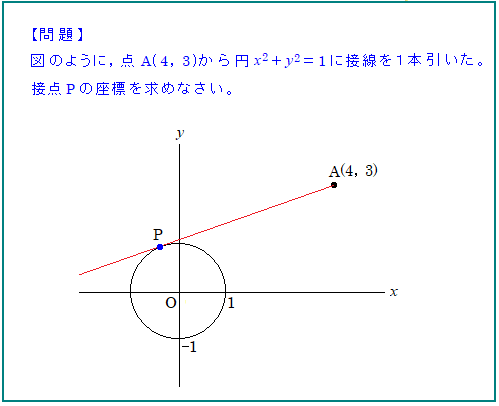
これは座標平面と言って、xとyの座標を1組として表した平面ですが、これを
複素数平面に置き換えて解く
と、うまくいくという例の為の問いです。
まずは普通に解く方法を2つほど。
続きを読む
高校数学Ⅲの「複素数平面」という分野の原稿を書いていて、
何とかすべて書き終えました。ふう・・。

この汚ない原稿は私が書いたもので、これを組版すると、
こうなる。

この瞬間が、この仕事のちょっと嬉しいときですね。
中高生にとって、もっともっと役に立つ良い本を作りたい。
こういう気持ちで仕事をしている。
あれれ・・この中に誤植がある・・。
今日はこういう、教科書にありそな問を1つ。

これは座標平面と言って、xとyの座標を1組として表した平面ですが、これを
複素数平面に置き換えて解く
と、うまくいくという例の為の問いです。
まずは普通に解く方法を2つほど。
続きを読む
2022年10月22日
複素数平面に強くなるには?
こんにちは。
しばらく更新途絶えました。多忙につき・・。
新宿、いつもの珈琲屋にて。

高校数学Ⅲの「複素数平面」という分野の原稿を書いていて、
あと少しとなりました。ふう・・。
とある入試問題を原稿に載せて解答を作ったあと、念のため
他社の解答を調べてみたら、答えが違っていた!!
たぶん私が間違っていると思ったけど、私は合っていた。
怖いですよね・・。
錯覚いけない、よく見るヨロシ。
教科書にも載っている有名な問を1つ。

綺麗な式ですよね、ほんと。
これ、本当に成り立つのか数値を当てはめてみた人いますか?

図のABCは1辺が2の正三角形になっていて、式を作ると上のようになり、
iの2乗は-1に置き換えて続きを計算すれば、確かに0になりますね。
ではどうやって等式を示すのか?

一般的なものはこの2つでしょうね。
①は大変なので、まずは②から。
続きを読む
しばらく更新途絶えました。多忙につき・・。
新宿、いつもの珈琲屋にて。

高校数学Ⅲの「複素数平面」という分野の原稿を書いていて、
あと少しとなりました。ふう・・。
とある入試問題を原稿に載せて解答を作ったあと、念のため
他社の解答を調べてみたら、答えが違っていた!!
たぶん私が間違っていると思ったけど、私は合っていた。
怖いですよね・・。
錯覚いけない、よく見るヨロシ。
教科書にも載っている有名な問を1つ。

綺麗な式ですよね、ほんと。
これ、本当に成り立つのか数値を当てはめてみた人いますか?

図のABCは1辺が2の正三角形になっていて、式を作ると上のようになり、
iの2乗は-1に置き換えて続きを計算すれば、確かに0になりますね。
ではどうやって等式を示すのか?

一般的なものはこの2つでしょうね。
①は大変なので、まずは②から。
続きを読む
2022年06月30日
相加・相乗・調和とは?
こんにちは。
連日暑いですね。
夏は苦手だ~~。とくに東京は暑い。
そーだ、涼しい長野に避暑しよう。
ところで、
Lineギフトというものがあるそうです。

これ、誰のケータイかは置いといて。
便利なもんですね。文化が進んで、我々の若い頃には無かった
人と仲良くなる方法が、いまは多々あります。
数学の話。
相加平均≧相乗平均≧調和平均
というのがあります。
これを証明する問題。

左から順に、相加、相乗、調和となるけど、
調和平均なんぞ、いつ使うのか?
問. 道を往復するのに、行きは時速4km、帰りは時速6kmで走った。
全体で、平均の速さは時速何kmか?
これはよくある引っ掛け問題で、(4+6)÷2とやるのは間違いで、

調和平均になるというのが、面白いです。
上の問題ですが、
対数を使った面白い証明方法を見つけたので、考えてみました。
続きを読む
連日暑いですね。
夏は苦手だ~~。とくに東京は暑い。
そーだ、涼しい長野に避暑しよう。
ところで、
Lineギフトというものがあるそうです。

これ、誰のケータイかは置いといて。
便利なもんですね。文化が進んで、我々の若い頃には無かった
人と仲良くなる方法が、いまは多々あります。
数学の話。
相加平均≧相乗平均≧調和平均
というのがあります。
これを証明する問題。

左から順に、相加、相乗、調和となるけど、
調和平均なんぞ、いつ使うのか?
問. 道を往復するのに、行きは時速4km、帰りは時速6kmで走った。
全体で、平均の速さは時速何kmか?
これはよくある引っ掛け問題で、(4+6)÷2とやるのは間違いで、

調和平均になるというのが、面白いです。
上の問題ですが、
対数を使った面白い証明方法を見つけたので、考えてみました。
続きを読む
2022年06月11日
連立方程式の解とは?
こんにちは。
土曜の午後。いつもの店にて。

甘いもの食べても、ちゃんとトレーニングすれば
太らないです。すれば、の話ですが。
数学の話。
連立方程式を解くことは中学で習うけど、例えば次の①、②を解く場合

③はともかく、④は引くところを足してしまった。
これでは解けないのだけど、
①と②を解く代わりに、③と④を解いてもいいのか?
つまり「①かつ②」と「③かつ④」が同値なのかどうか?
こういうことは中学で教わらないし、高校でもあまり触れない。
連立方程式をイチから解くことを考えてみました。

文字ばかりでややこしくて、ちゃんと解くのは大変でした。
答えを見る前に自分で解いてみるとか、やめましょう。
「定数」というのは定まった数であるのに、実はどんな値でも
とり得るものなので、自分の都合で設定できない。
だから、文字が0になることも考えなくてはいけなくて、厄介です。
変形していくとき、どの式とどの式が同値なのか?
つくった式の係数や、定数項が0であるかどうか?
こういうことを気にしなくてはいけない。だから大変でした。
続きを読む
土曜の午後。いつもの店にて。

甘いもの食べても、ちゃんとトレーニングすれば
太らないです。すれば、の話ですが。
数学の話。
連立方程式を解くことは中学で習うけど、例えば次の①、②を解く場合

③はともかく、④は引くところを足してしまった。
これでは解けないのだけど、
①と②を解く代わりに、③と④を解いてもいいのか?
つまり「①かつ②」と「③かつ④」が同値なのかどうか?
こういうことは中学で教わらないし、高校でもあまり触れない。
連立方程式をイチから解くことを考えてみました。

文字ばかりでややこしくて、ちゃんと解くのは大変でした。
答えを見る前に自分で解いてみるとか、やめましょう。
「定数」というのは定まった数であるのに、実はどんな値でも
とり得るものなので、自分の都合で設定できない。
だから、文字が0になることも考えなくてはいけなくて、厄介です。
変形していくとき、どの式とどの式が同値なのか?
つくった式の係数や、定数項が0であるかどうか?
こういうことを気にしなくてはいけない。だから大変でした。
続きを読む
2022年01月01日
2021年12月12日
みかんを配るには?
こんにちは。
今年も残りわずか。
東京に越して3年目の冬なのだけど、冬は、
実家の長野に比べて暖かいので心配ないです。
数学の会社を経営して3年。
今年1年はそれなりに仕事が入ったのだけど、
売り上げはイマイチだったかな。まあ想定内です。

お世話になっている会社からお歳暮が届いた。
温州=うんしゅう
と読むようです。
こりゃうまいですね~。
みかんの問題を作りました。

隣の人にみかんを1個も渡さない、という場合もあってよいことにします。
Mを最小にしたいのだから、隣の人に渡したあとその人からもらっていては、
移動するみかんが重複して割が悪いですね。なので、

このように時計回りに渡していくとして、各自が10個になるようにxで表します。
渡す個数は負の数でもOKで、そのときは反対にみかんをもらうことになります。
「移動するみかんの個数の合計」なので、負の数は正にして足さないといけない。
なかなか簡単でないです。
続きを読む
今年も残りわずか。
東京に越して3年目の冬なのだけど、冬は、
実家の長野に比べて暖かいので心配ないです。
数学の会社を経営して3年。
今年1年はそれなりに仕事が入ったのだけど、
売り上げはイマイチだったかな。まあ想定内です。

お世話になっている会社からお歳暮が届いた。
温州=うんしゅう
と読むようです。
こりゃうまいですね~。
みかんの問題を作りました。

隣の人にみかんを1個も渡さない、という場合もあってよいことにします。
Mを最小にしたいのだから、隣の人に渡したあとその人からもらっていては、
移動するみかんが重複して割が悪いですね。なので、

このように時計回りに渡していくとして、各自が10個になるようにxで表します。
渡す個数は負の数でもOKで、そのときは反対にみかんをもらうことになります。
「移動するみかんの個数の合計」なので、負の数は正にして足さないといけない。
なかなか簡単でないです。
続きを読む
2021年12月03日
計算に強くなるには?
こんにちは。
もう12月ですか、早いですね。
来年の受験まであとわずかです。
会社の書棚にあった、ずいぶん古い参考書たち。

昭和●年とか書いてある。
チャートは私が高校の頃は赤と青しかなくて、写真と同じ小さい版だった。
赤は鬼のようにムズかった・・。
チャートに載っていた問を解いてみますか。

(1)は全部展開しても解けるのだけど、やる気がしないですね。
かっこの中を置き換えてみようか、という気になります。
文字の置き換えで、簡単化をはかる
(2)は文字を1つ消して解くという方法だと、ルートがついてしまって、
たぶん解けないですね。
対称形 → x+y=u、xy=vとおけ
この赤字は本に書いてあります。
こういうキャッチなコピーが実にうまい。
続きを読む
もう12月ですか、早いですね。
来年の受験まであとわずかです。
会社の書棚にあった、ずいぶん古い参考書たち。

昭和●年とか書いてある。
チャートは私が高校の頃は赤と青しかなくて、写真と同じ小さい版だった。
赤は鬼のようにムズかった・・。
チャートに載っていた問を解いてみますか。

(1)は全部展開しても解けるのだけど、やる気がしないですね。
かっこの中を置き換えてみようか、という気になります。
文字の置き換えで、簡単化をはかる
(2)は文字を1つ消して解くという方法だと、ルートがついてしまって、
たぶん解けないですね。
対称形 → x+y=u、xy=vとおけ
この赤字は本に書いてあります。
こういうキャッチなコピーが実にうまい。
続きを読む
2021年11月12日
ロックか水割りか?
こんにちは。
とあるBARにて。

ウイスキーには何種類かあるのだけど、代表的なのが
スコッチ と バーボン
どちらも原料は麦だけど、バーボンにはとうもろこしを含む。
これがカラメルのような甘い味を引き出すわけですな。
ロックにします?それかソーダで割りますか?
バーテンがお酒のウンチクを語ってくれる。
都会の雑踏の中、しばしの安らぎと言ったところ。
数学の話。
中学の連立方程式の文章題で、よくあるのが食塩水の問題。
問題
5%の食塩水Aと8%の食塩水Bを混ぜたら、
6%の食塩水が300gできた。それぞれ何g混ぜたか。
これは次のように連立方程式を立てて解けばいい。
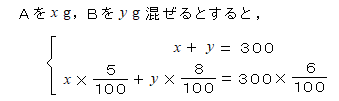
しかし、方程式を立てないで解く方法もあります。

この解き方は「天びん法」とか言うようで、
学校では習わないけど、中学受験の小6生は塾で習う。
なぜこの方法で答えが求まるのか?
これを考えてみました。
続きを読む
とあるBARにて。

ウイスキーには何種類かあるのだけど、代表的なのが
スコッチ と バーボン
どちらも原料は麦だけど、バーボンにはとうもろこしを含む。
これがカラメルのような甘い味を引き出すわけですな。
ロックにします?それかソーダで割りますか?
バーテンがお酒のウンチクを語ってくれる。
都会の雑踏の中、しばしの安らぎと言ったところ。
数学の話。
中学の連立方程式の文章題で、よくあるのが食塩水の問題。
問題
5%の食塩水Aと8%の食塩水Bを混ぜたら、
6%の食塩水が300gできた。それぞれ何g混ぜたか。
これは次のように連立方程式を立てて解けばいい。
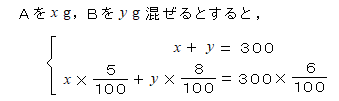
しかし、方程式を立てないで解く方法もあります。

この解き方は「天びん法」とか言うようで、
学校では習わないけど、中学受験の小6生は塾で習う。
なぜこの方法で答えが求まるのか?
これを考えてみました。
続きを読む
2021年09月06日
ピタゴラス数(その3)
こんにちは。
都内まだまだコロナ騒ぎが収まらず。
実家にはなかなか帰省できないし、しても街のレストランは
県外の人お断りと書かれているし・・。
普通に暮らせるのはいつだろーか?

ウチの畑にある木です。この実の名は?
ヒント:ぴりりと辛い。
数学の話。
ピタゴラス数とは、直角三角形の3辺が全部整数になるときの
その数の組のことで、案外無いようで、実は無限にあります。
その1
その2
これの続きです。


ピタゴラス数のうち、上のように最大公約数が1のものを
原始ピタゴラス数といいます。特徴を挙げると次のようです。
1)a、bのうち一方は偶数、他方は奇数
2)a、bのうち一方は3の倍数
3)a、bのうち一方は4の倍数
4)a、b、cのうちいずれかは5の倍数
5)面積は6の整数倍
6)内接円の半径は必ず整数
このうちの3)を考えます。検索すればいろいろ証明法が出てくるけど、
たぶん載ってないと思う解法をここに載せよう。
続きを読む
都内まだまだコロナ騒ぎが収まらず。
実家にはなかなか帰省できないし、しても街のレストランは
県外の人お断りと書かれているし・・。
普通に暮らせるのはいつだろーか?

ウチの畑にある木です。この実の名は?
ヒント:ぴりりと辛い。
数学の話。
ピタゴラス数とは、直角三角形の3辺が全部整数になるときの
その数の組のことで、案外無いようで、実は無限にあります。
その1
その2
これの続きです。


ピタゴラス数のうち、上のように最大公約数が1のものを
原始ピタゴラス数といいます。特徴を挙げると次のようです。
1)a、bのうち一方は偶数、他方は奇数
2)a、bのうち一方は3の倍数
3)a、bのうち一方は4の倍数
4)a、b、cのうちいずれかは5の倍数
5)面積は6の整数倍
6)内接円の半径は必ず整数
このうちの3)を考えます。検索すればいろいろ証明法が出てくるけど、
たぶん載ってないと思う解法をここに載せよう。
続きを読む
2021年09月01日
ピタゴラス数(その2)
こんにちは。
東京は銀座にて。

「カードで。」
万年筆は外国産の方がいろいろオシャレですね。
数学の話。
ピタゴラス数とは、直角三角形の3辺が全部整数になるときの
その数の組のことで、案外無いようで、実は無限にあります。
求め方はこちら。
今日は前回と違う解き方を考えました。

当て推量で探すのでなく、一般形を作ってから求めたい。
直角をはさむ2辺のうち奇数の方に着目し、三平方の定理を次のように変形します。

ここから一般形が作れないだろーか?
いろいろ悩んで、何とか結論が出ました。
続きを読む
東京は銀座にて。

「カードで。」
万年筆は外国産の方がいろいろオシャレですね。
数学の話。
ピタゴラス数とは、直角三角形の3辺が全部整数になるときの
その数の組のことで、案外無いようで、実は無限にあります。
求め方はこちら。
今日は前回と違う解き方を考えました。

当て推量で探すのでなく、一般形を作ってから求めたい。
直角をはさむ2辺のうち奇数の方に着目し、三平方の定理を次のように変形します。

ここから一般形が作れないだろーか?
いろいろ悩んで、何とか結論が出ました。
続きを読む
2021年08月27日
重心の不等式。
こんにちは。
長野から東京に単身上京して会社を経営し、2年が過ぎた。
都会と田舎の違い、これは結構ありますね。何が違うか?
1)体感する刺激・・・都会の方が多様化していて刺激が多い。
2)時間の感覚・・・・都会はせわしい、田舎はのんびり。と言った感。
3)めんどくささ・・・・田舎は地域の中で役割がある。都会は何も無い。
このあたりですかね。
仕事は楽でないけど、まあ楽しいです今のところ。
今週考えていた問題がこちら。

美しい式だ。
線分の長さは2乗しないとルートがついてしまうので、このままの形では証明しにくいです。
AO、BO、COをRとおいて、
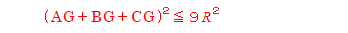
これを示せばいいのだけど、すぐにはできない。

こういう感じで中継する式が必要です。
これは大変だ・・。
続きを読む
長野から東京に単身上京して会社を経営し、2年が過ぎた。
都会と田舎の違い、これは結構ありますね。何が違うか?
1)体感する刺激・・・都会の方が多様化していて刺激が多い。
2)時間の感覚・・・・都会はせわしい、田舎はのんびり。と言った感。
3)めんどくささ・・・・田舎は地域の中で役割がある。都会は何も無い。
このあたりですかね。
仕事は楽でないけど、まあ楽しいです今のところ。
今週考えていた問題がこちら。

美しい式だ。
線分の長さは2乗しないとルートがついてしまうので、このままの形では証明しにくいです。
AO、BO、COをRとおいて、
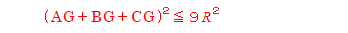
これを示せばいいのだけど、すぐにはできない。

こういう感じで中継する式が必要です。
これは大変だ・・。
続きを読む





