2025年03月23日
2025早大・商(第1問の4)
こんにちは。
引き続き、早大商学部。

今日は(4)です。
難問だ。正9角形が馴染みが無い。60°の角度がどうやって作られるか?
ここをまず調べるしかないですね。
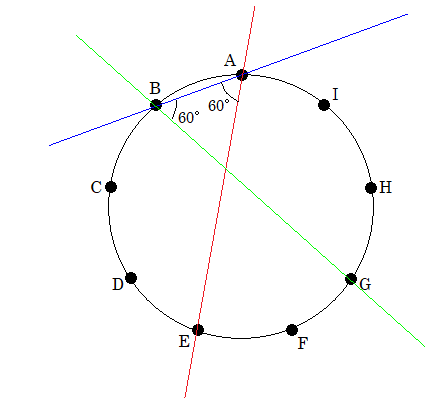
円を描いて、円周角を考えるといいです。
図のような赤、青、緑の線をひくと、正三角形ができます。
あとはこれらの直線を平行移動しても同じ60°の角ができる。
こんな感じで数えていきます。
続きを読む
引き続き、早大商学部。

今日は(4)です。
難問だ。正9角形が馴染みが無い。60°の角度がどうやって作られるか?
ここをまず調べるしかないですね。

円を描いて、円周角を考えるといいです。
図のような赤、青、緑の線をひくと、正三角形ができます。
あとはこれらの直線を平行移動しても同じ60°の角ができる。
こんな感じで数えていきます。
続きを読む
2025年03月22日
2025早大・商(第1問の3)
こんにちは。
天気の良い土曜日。
久々のオフだ。
休日引き続き、早大商学部。

今日は(3)です。
「等式を満たす」ということは、等式がxについての恒等式になるということです。
なのでm、nは任意でなく何か特定の数になるはずで、そこで両辺の次数を調べれば
m、nの条件が出て、値が決まるかな・・?
と、考えるところです。
続きを読む
天気の良い土曜日。
久々のオフだ。
休日引き続き、早大商学部。

今日は(3)です。
「等式を満たす」ということは、等式がxについての恒等式になるということです。
なのでm、nは任意でなく何か特定の数になるはずで、そこで両辺の次数を調べれば
m、nの条件が出て、値が決まるかな・・?
と、考えるところです。
続きを読む
2025年03月22日
2025早大・商(第1問の2)
こんにちは。
引き続き、早大商学部。

今日は(2)のみです。
3項間漸化式で、よくある形なのでそれほど難でない。
しかしa2でなくa2025が0というのが作為的ですな。
これ、0にしてくれているので案外ラクに解けます。
続きを読む
引き続き、早大商学部。

今日は(2)のみです。
3項間漸化式で、よくある形なのでそれほど難でない。
しかしa2でなくa2025が0というのが作為的ですな。
これ、0にしてくれているので案外ラクに解けます。
続きを読む
2025年03月20日
2025早大・商(第1問の1)
こんにちは。
もう3月か、早いですね。
いろんな入試が終わった、こういうとき仕事がカブるもので、
この時期は休みが無い。

行き付けの店にて。社長なので会社の経費で飲む。
これだけですな、社長やってて良いなと思うことは・・。
早稲田の商学部。
文系なのに数学が難しく、60点満点で平均が10点そこそこらしい。
どんな問が出てるのか見てみたら、なかなかだった。
面白いので解いてみますか。

大問1は小問集合4問だけど、どれも簡単でない。
今日は(1)のみです。
だいたい2つ式があるときはyを消してxの方程式を作るのだけど、
直接図を描くと、こうなるかな。
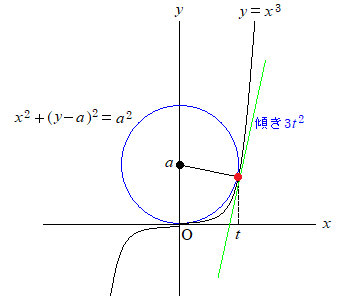
この図以外に共有点が2個になる場合が無いことを示す必要があるけど、
まあ細かいことは置いといて、式はこうなる。

この連立方程式を解けば一応答えは出るけど、あまりうまい解き方でない。
解答は、yを消す方法で。
続きを読む
もう3月か、早いですね。
いろんな入試が終わった、こういうとき仕事がカブるもので、
この時期は休みが無い。

行き付けの店にて。社長なので会社の経費で飲む。
これだけですな、社長やってて良いなと思うことは・・。
早稲田の商学部。
文系なのに数学が難しく、60点満点で平均が10点そこそこらしい。
どんな問が出てるのか見てみたら、なかなかだった。
面白いので解いてみますか。

大問1は小問集合4問だけど、どれも簡単でない。
今日は(1)のみです。
だいたい2つ式があるときはyを消してxの方程式を作るのだけど、
直接図を描くと、こうなるかな。

この図以外に共有点が2個になる場合が無いことを示す必要があるけど、
まあ細かいことは置いといて、式はこうなる。

この連立方程式を解けば一応答えは出るけど、あまりうまい解き方でない。
解答は、yを消す方法で。
続きを読む
2025年03月03日
2025東大・文系(第4問)
こんにちは。
引き続き東大文系。
最終の第4問は、面積の問題。

見た感じ対して難しくなさそうで、実際にそれほど難ではない。
しかし場合分けが多く、いちいち全部面積を求めていくと大変すぎる。
aを正として徐々に大きくしていくと、
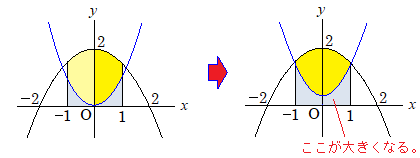
面積は小さくなっていくことがわかる。
aが負のときは絶対値のグラフが折り返されるのでややこしい。
-2から徐々に大きくしていくと、
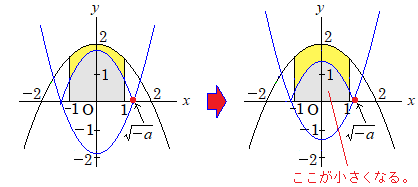
x軸との交点が±1の外にあれば、面積が大きくなっていくことがわかる。
これらを排除すれば、あとは-1≦a≦0のときを調べるだけでよくなる。
なかなか面倒な問だ。
続きを読む
引き続き東大文系。
最終の第4問は、面積の問題。

見た感じ対して難しくなさそうで、実際にそれほど難ではない。
しかし場合分けが多く、いちいち全部面積を求めていくと大変すぎる。
aを正として徐々に大きくしていくと、

面積は小さくなっていくことがわかる。
aが負のときは絶対値のグラフが折り返されるのでややこしい。
-2から徐々に大きくしていくと、

x軸との交点が±1の外にあれば、面積が大きくなっていくことがわかる。
これらを排除すれば、あとは-1≦a≦0のときを調べるだけでよくなる。
なかなか面倒な問だ。
続きを読む
2025年02月27日
2025東大・文系(第3問)
こんにちは。
引き続き東大文系。
第3問は確率の問題。これが一番難だった。

(2)は漸化式を作るタイプの問だろうと予測できるが、
どうやって式を立てればよいか?ここが相当ムズい。
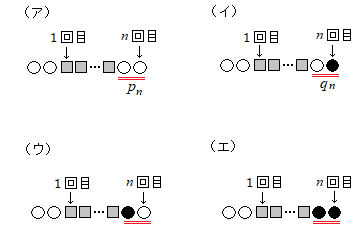
右から1番目と2番目の2個の玉のパターンはこの4つで、
アの確率pnとイの確率qnの和が(2)の答えになる。なので、
まずはpnとqnの関係式を作ろうかと考えるのが手順ですね。
続きを読む
引き続き東大文系。
第3問は確率の問題。これが一番難だった。

(2)は漸化式を作るタイプの問だろうと予測できるが、
どうやって式を立てればよいか?ここが相当ムズい。

右から1番目と2番目の2個の玉のパターンはこの4つで、
アの確率pnとイの確率qnの和が(2)の答えになる。なので、
まずはpnとqnの関係式を作ろうかと考えるのが手順ですね。
続きを読む
2025年02月27日
2025東大・文系(第2問)
こんにちは。
国立大の2次試験、昨日から始まりました。
引き続き東大文系、ゆうべ一応全部解けたけど、
やっぱどれも簡単でないですね。
第2問は図形の問題。

まずM、Nを中点、Oを外心として、小さめの円を描いてみる。
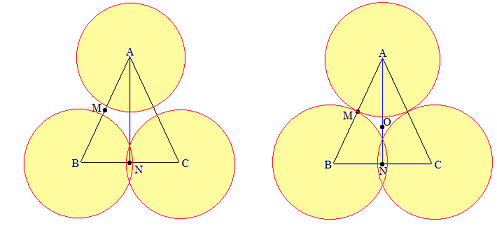
左図は、辺ABとACの一部がDrに含まれていない。
右図は、3辺がみなDrに含まれているが、Oの周りが含まれていない。
中点や外心を取ることに気付けるかどうか。
あと、鈍角三角形のときは外心が外に出るので解が違う。
なかなか面倒な問題だ・・。
続きを読む
国立大の2次試験、昨日から始まりました。
引き続き東大文系、ゆうべ一応全部解けたけど、
やっぱどれも簡単でないですね。
第2問は図形の問題。

まずM、Nを中点、Oを外心として、小さめの円を描いてみる。

左図は、辺ABとACの一部がDrに含まれていない。
右図は、3辺がみなDrに含まれているが、Oの周りが含まれていない。
中点や外心を取ることに気付けるかどうか。
あと、鈍角三角形のときは外心が外に出るので解が違う。
なかなか面倒な問題だ・・。
続きを読む
2025年02月25日
2025東大・文系(第1問)
こんにちは。
国立大の2次試験、本日から始まりました。
私はもう塾の先生でないので、受験生の心配は無い。
なので、のんびり解いていこうかと思います。
今年の東大。文系の方です。

(2)のほう、図をかくとこんな感じです。
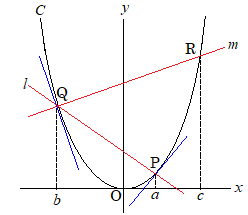
これ、PからQ、QからRと同じことをしているので、
b=(aの式)
を作ったら、c=(bの式)も同じ形になります。
これに気づけると二度手間が防げる。
しかし対象となるものが分数関数なので、どう処理するのか?
ここがややムズいです。
続きを読む
国立大の2次試験、本日から始まりました。
私はもう塾の先生でないので、受験生の心配は無い。
なので、のんびり解いていこうかと思います。
今年の東大。文系の方です。

(2)のほう、図をかくとこんな感じです。

これ、PからQ、QからRと同じことをしているので、
b=(aの式)
を作ったら、c=(bの式)も同じ形になります。
これに気づけると二度手間が防げる。
しかし対象となるものが分数関数なので、どう処理するのか?
ここがややムズいです。
続きを読む
2025年01月12日
2025共通テスト試作問題(数2BC)
こんにちは。
あと1週間ですね、共通テストが。
試作問題。こちら。
数2BCの第7問、これは数Cの問です。
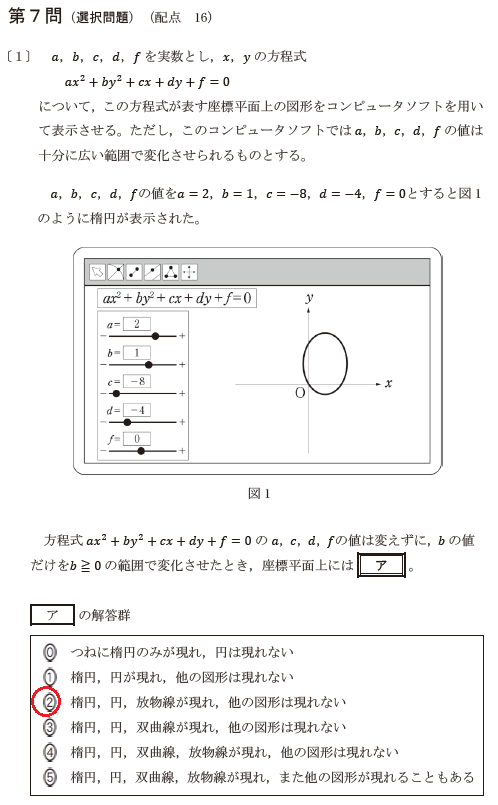
2次曲線はaとbの符号で形が決まる。それを知っていれば易しい。
続いて、〔2〕です。
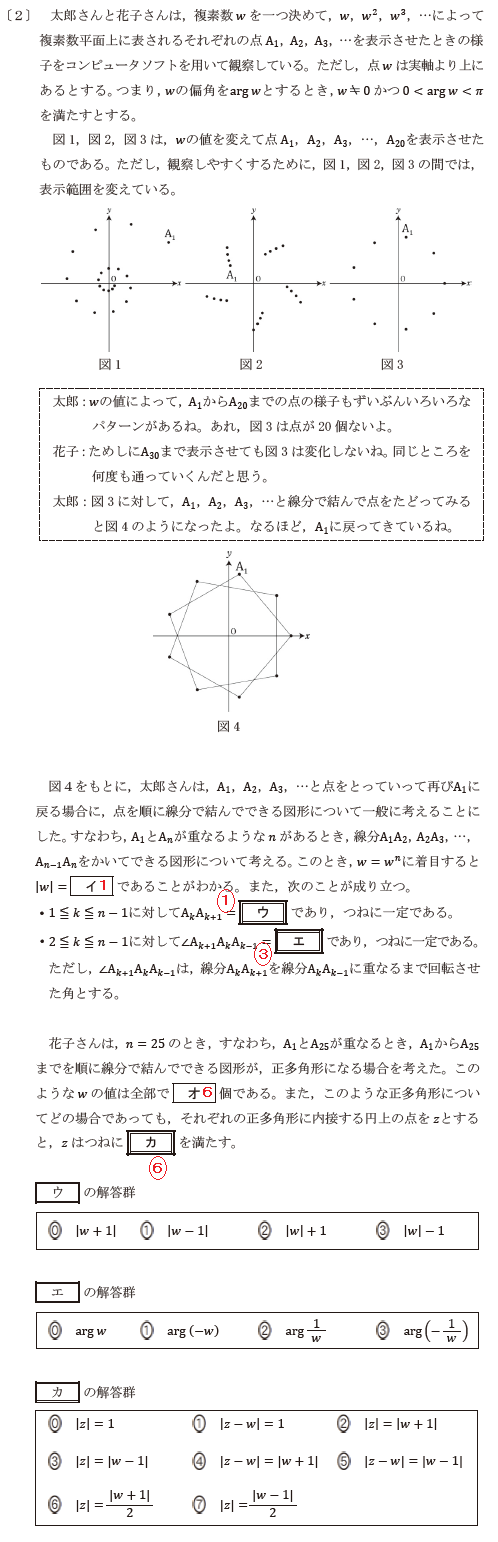
この問の図1と図2は、問題を解くのに全く必要としない。
こういう不要な情報をあえて入れてくるのも共通テストの特徴の1つかと思う。
続きを読む
あと1週間ですね、共通テストが。
試作問題。こちら。
数2BCの第7問、これは数Cの問です。

2次曲線はaとbの符号で形が決まる。それを知っていれば易しい。
続いて、〔2〕です。

この問の図1と図2は、問題を解くのに全く必要としない。
こういう不要な情報をあえて入れてくるのも共通テストの特徴の1つかと思う。
続きを読む
2025年01月11日
2025共通テスト試作問題(数1A)
こんにちは。
あと1週間ですね、共通テストが。
この試験の数学なのだけど、毎回解くたびに腹が立ってしまう。
文章がえらく長く、それが物語になっていて読解に苦労すること。
考え方を指定してそれに乗る必要があり、自由に発想できないこと。
答えが選択肢になるケースがあり、これを選ぶのがめんどいこと。
など。こういうことを分かったうえで根気よくしかもスピーディに
解く必要がありますね。もっとシンプルにできないものか・・?
数学の能力以外のとこで差がついてしまうのではと毎回思う。
試験問題はこういう感じになりますよ、というものがUPされていたので、
解いてみますか。こちら。
数1Aの第4問で、確率の問です。

ここまでは2021年の共通テスト1A第3問とほぼ同じです。
全4ページ。うんざりですな・・。
後半は文章量が多い割に設問が少ない。途中の会話文は、問題を解くうえで
ヒントになっているので読み飛ばさないほうがいい。
スセ以降が難しい。
一見、XとYのどちらを取っても期待値は変わらないように見えるけど、
太郎の試行で結果が1つ出ているので、それが花子の選択に影響しているというのが、
この問題の主旨となっている。厄介だ・・。
続きを読む
あと1週間ですね、共通テストが。
この試験の数学なのだけど、毎回解くたびに腹が立ってしまう。
文章がえらく長く、それが物語になっていて読解に苦労すること。
考え方を指定してそれに乗る必要があり、自由に発想できないこと。
答えが選択肢になるケースがあり、これを選ぶのがめんどいこと。
など。こういうことを分かったうえで根気よくしかもスピーディに
解く必要がありますね。もっとシンプルにできないものか・・?
数学の能力以外のとこで差がついてしまうのではと毎回思う。
試験問題はこういう感じになりますよ、というものがUPされていたので、
解いてみますか。こちら。
数1Aの第4問で、確率の問です。

ここまでは2021年の共通テスト1A第3問とほぼ同じです。

全4ページ。うんざりですな・・。
後半は文章量が多い割に設問が少ない。途中の会話文は、問題を解くうえで
ヒントになっているので読み飛ばさないほうがいい。
スセ以降が難しい。
一見、XとYのどちらを取っても期待値は変わらないように見えるけど、
太郎の試行で結果が1つ出ているので、それが花子の選択に影響しているというのが、
この問題の主旨となっている。厄介だ・・。
続きを読む
2024年03月16日
2024灘中学入試・算数(その6)
こんにちは。
灘中入試、引き続き。
第8問からは図形の問が続く。

算数では長さが等しいことを等式で書かないので、見づらい。
AE=AFを見逃してしまい、解けない問をずっと考えておりました。
EF=BCがいえるのだけど、なぜなのか?
とても小学校の算数では説明できないな。
試験中に証明している時間が惜しいし、三角形が何となく合同だから等しい、
という感じで解くのでしょうね。
続きを読む
灘中入試、引き続き。
第8問からは図形の問が続く。

算数では長さが等しいことを等式で書かないので、見づらい。
AE=AFを見逃してしまい、解けない問をずっと考えておりました。
EF=BCがいえるのだけど、なぜなのか?
とても小学校の算数では説明できないな。
試験中に証明している時間が惜しいし、三角形が何となく合同だから等しい、
という感じで解くのでしょうね。
続きを読む
2024年03月11日
2024灘中学入試・算数(その5)
こんにちは。
灘中入試、引き続き。
第7問は、数え上げの問題。

電球が点灯するのは、スイッチがonになった道ができる場合で、
その道が複数できるときもあるし、これはなかなか厄介です。
策1 点灯する場合を全部数え上げる
策2 点灯しない場合を数え上げ、128から引く
このどちらがよいか?やってみないとわからないけど、
場合分けの方法として、下2つのonとoffで分けてみる。

Aが消えてBがつく場合は、真ん中の場合と同じなので略でいい。
策1は左の場合が大変そうなので、策2で行くことにした。
続きを読む
灘中入試、引き続き。
第7問は、数え上げの問題。

電球が点灯するのは、スイッチがonになった道ができる場合で、
その道が複数できるときもあるし、これはなかなか厄介です。
策1 点灯する場合を全部数え上げる
策2 点灯しない場合を数え上げ、128から引く
このどちらがよいか?やってみないとわからないけど、
場合分けの方法として、下2つのonとoffで分けてみる。

Aが消えてBがつく場合は、真ん中の場合と同じなので略でいい。
策1は左の場合が大変そうなので、策2で行くことにした。
続きを読む
2024年03月07日
2024灘中学入試・算数(その4)
こんにちは。
灘中入試、引き続き。
第6問は、数の性質をうまく活用した面白い問題。

4桁の数ABCDが何個できるかというと、8C4だから70通り。
1つずつ順に調べて条件に合うかを見ればいいけど、
その場合、平均何回で見つかるか?
期待値を計算するとおよそ35回となります。試験中にやる気になれないですね。
この問で着目することが、次のこと。
A+B+・・+H=1+2+・・+8=36
9の倍数になっているので、これを手掛かりにします。
次は、4桁の数が9の倍数になるための条件です。

この性質は是非知っておくべきことですね。
続きを読む
灘中入試、引き続き。
第6問は、数の性質をうまく活用した面白い問題。

4桁の数ABCDが何個できるかというと、8C4だから70通り。
1つずつ順に調べて条件に合うかを見ればいいけど、
その場合、平均何回で見つかるか?
期待値を計算するとおよそ35回となります。試験中にやる気になれないですね。
この問で着目することが、次のこと。
A+B+・・+H=1+2+・・+8=36
9の倍数になっているので、これを手掛かりにします。
次は、4桁の数が9の倍数になるための条件です。

この性質は是非知っておくべきことですね。
続きを読む
2024年03月06日
2024灘中学入試・算数(その3)
こんにちは。
3月に入ったけど、東京はまだ寒い。
灘中入試、引き続き。

整数が11の倍数になるのは、各位がどんなときか?
この性質を知らないと、しらみつぶしに調べることになるのでキツい。
作者はそのことを見越して出題したのだろーか?
小6生でもわかるように、性質と証明を書いた。

これを使ってよいことにして解答を作った。
続きを読む
3月に入ったけど、東京はまだ寒い。
灘中入試、引き続き。

整数が11の倍数になるのは、各位がどんなときか?
この性質を知らないと、しらみつぶしに調べることになるのでキツい。
作者はそのことを見越して出題したのだろーか?
小6生でもわかるように、性質と証明を書いた。

これを使ってよいことにして解答を作った。
続きを読む
2024年03月05日
2024灘中学入試・算数(その2)
こんにちは。
灘中学の入試問題。
引き続き解いていきます。
これは小6生が解く問題なので、
なるべく算数だけで解こうと思う。

高校の数学Aの中に「集合の要素の個数」という単元があって、こういう図をかいて考えます。
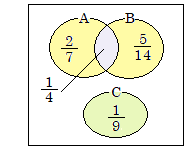
n(A∪B)=n(A)+n(B)-n(A∩B)
式で書くとこうなるけど、意味を説明すれば小6生でもわかると思う。
もう1問。

旅人算
の中に、出会い算とか追いつき算とかがある。
そのたぐいかなと思ったけど、条件が3つあるので何かヘンですね。
逆向きに走る2パターンだけを考えたら、解けてしまった・・。
何か勘違いしたのだろーか?
続きを読む
灘中学の入試問題。
引き続き解いていきます。
これは小6生が解く問題なので、
なるべく算数だけで解こうと思う。

高校の数学Aの中に「集合の要素の個数」という単元があって、こういう図をかいて考えます。

n(A∪B)=n(A)+n(B)-n(A∩B)
式で書くとこうなるけど、意味を説明すれば小6生でもわかると思う。
もう1問。

旅人算
の中に、出会い算とか追いつき算とかがある。
そのたぐいかなと思ったけど、条件が3つあるので何かヘンですね。
逆向きに走る2パターンだけを考えたら、解けてしまった・・。
何か勘違いしたのだろーか?
続きを読む
2024年03月04日
2024灘中学入試・算数(その1)
こんにちは。
受験の季節。
私の会社は数学の会社で、この時期は入試の仕事が入ってくる。
とにかく毎日数学の問を解きまくる仕事であって、こういうのは
好きでないとできないですね。
私は問題解くのが趣味なので、何も苦でないです。
中学入試の仕事は無いけど、毎年解いているので
今年も解きますか。

1日目は全12問。
中学入試なので小6生が解く問題なのだけど、何だか高校入試に出ても
おかしくない問題が後半に多々ある。
最初はウォーミングアップかなと思いきや、結構面倒な計算。

特に工夫する手もなく、ただ計算すればいい。
2番は、中1の1次方程式の文章題にちょうどいい問題で、
求めるものをx円として、
5x-120=7(x-100)+60
これを解けばいい。
でも小6生がわかるような解き方で解いた。
続きを読む
受験の季節。
私の会社は数学の会社で、この時期は入試の仕事が入ってくる。
とにかく毎日数学の問を解きまくる仕事であって、こういうのは
好きでないとできないですね。
私は問題解くのが趣味なので、何も苦でないです。
中学入試の仕事は無いけど、毎年解いているので
今年も解きますか。

1日目は全12問。
中学入試なので小6生が解く問題なのだけど、何だか高校入試に出ても
おかしくない問題が後半に多々ある。
最初はウォーミングアップかなと思いきや、結構面倒な計算。

特に工夫する手もなく、ただ計算すればいい。
2番は、中1の1次方程式の文章題にちょうどいい問題で、
求めるものをx円として、
5x-120=7(x-100)+60
これを解けばいい。
でも小6生がわかるような解き方で解いた。
続きを読む
2024年02月29日
2024東大・文系(第4問)
こんにちは。
引き続き、東大文系。
最終問題は確率でした。

確率をnの式で表す問題。こういうときは、まず小さいnで調べてみるのが
第一歩です。奇数なので5と7を描くと、こうなる。

n=5のときはどの場合もOを内部に含むので、確率は1ですね。
n=7のときは、Oを内部に含まない場合はあるけど、そう多くない。
pn=1-(Oを内部に含まない確率)
余事象を考える方がラクそうです。とはいえ、数え方がややこしい。
漏れなく重複なく数えるのに図のAを固定するのかしないのか?
あと、Oを内部に含まない場合をどうやって数えるのか?
数え方に工夫が要りますね・・。
続きを読む
引き続き、東大文系。
最終問題は確率でした。

確率をnの式で表す問題。こういうときは、まず小さいnで調べてみるのが
第一歩です。奇数なので5と7を描くと、こうなる。

n=5のときはどの場合もOを内部に含むので、確率は1ですね。
n=7のときは、Oを内部に含まない場合はあるけど、そう多くない。
pn=1-(Oを内部に含まない確率)
余事象を考える方がラクそうです。とはいえ、数え方がややこしい。
漏れなく重複なく数えるのに図のAを固定するのかしないのか?
あと、Oを内部に含まない場合をどうやって数えるのか?
数え方に工夫が要りますね・・。
続きを読む
2024年02月28日
2024東大・文系(第3問)
こんにちは。
引き続き、東大文系。
第3問は座標平面上の図形の問題。

図を描くとこうなる。
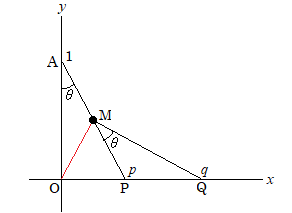
赤い線は何となく引いてみた。直角三角形の斜辺の中点は外心だから、
AM=PM=OMとなる。この条件が使えるかもだし、意味ないかもしれないが・・。
(1)が解ければ、(2)(3)は方程式、不等式を解くだけなので易しい。
なので(1)が解けるかどうかがカギになりますね。
続きを読む
引き続き、東大文系。
第3問は座標平面上の図形の問題。

図を描くとこうなる。

赤い線は何となく引いてみた。直角三角形の斜辺の中点は外心だから、
AM=PM=OMとなる。この条件が使えるかもだし、意味ないかもしれないが・・。
(1)が解ければ、(2)(3)は方程式、不等式を解くだけなので易しい。
なので(1)が解けるかどうかがカギになりますね。
続きを読む
2024年02月27日
2024東大・文系(第2問)
こんにちは。
引き続き、東大文系。
第2問は珍しい指数対数の問題。

(1)はどの参考書にもあるタイプの問で易しい。
(2)が困ってしまうな・・。見たことない形でしょう。
直接両辺の対数を取るのは、左辺が和だからうまく行かない。
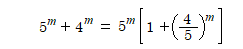
こういう変形はどうか?これも[ ]の中の処理が困る。
仕方ないのでmに値を入れて調べよーか?こう考えた人いませんか?
m=4のとき、左辺=625+256=3桁
m=5のとき、左辺=3125+1024=4桁
m=6のとき、左辺=15625+4096=5桁
m=7のとき、左辺=78125+16384=5桁
m=8のとき、左辺=390625+65536=6桁
m=9のとき、左辺=1953125+262144=7桁
こんなことしていては、答えを出すまでに試験が終わってしまう。
しかし、これを見て気づいてしまった。
左辺の桁数は、4^mが足されたところで変わらない。
なので答えが見えた感じですね。
続きを読む
引き続き、東大文系。
第2問は珍しい指数対数の問題。

(1)はどの参考書にもあるタイプの問で易しい。
(2)が困ってしまうな・・。見たことない形でしょう。
直接両辺の対数を取るのは、左辺が和だからうまく行かない。
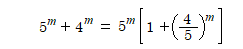
こういう変形はどうか?これも[ ]の中の処理が困る。
仕方ないのでmに値を入れて調べよーか?こう考えた人いませんか?
m=4のとき、左辺=625+256=3桁
m=5のとき、左辺=3125+1024=4桁
m=6のとき、左辺=15625+4096=5桁
m=7のとき、左辺=78125+16384=5桁
m=8のとき、左辺=390625+65536=6桁
m=9のとき、左辺=1953125+262144=7桁
こんなことしていては、答えを出すまでに試験が終わってしまう。
しかし、これを見て気づいてしまった。
左辺の桁数は、4^mが足されたところで変わらない。
なので答えが見えた感じですね。
続きを読む
2024年02月26日
2024東大・文系(第1問)
こんにちは。
国立大の2次試験、昨日から始まったようです。
塾の先生ももうやってないので受験生の心配がない。
なのでのんびり解こうかと思います。

解答集の難易には[標準]と書かれそうな、よくある感じの問題だけど、
(3)で不等式があるのが珍しい感じです。
図を描くと、こうです。

PとQがy軸対称なので、Cもy軸対称。よってb=0
となりそうだけど、これは証明した方が無難ですね。
(3)は、求めたAの式が複雑になるので、どうやって示すか?
その選択が大事なところです。
続きを読む
国立大の2次試験、昨日から始まったようです。
塾の先生ももうやってないので受験生の心配がない。
なのでのんびり解こうかと思います。

解答集の難易には[標準]と書かれそうな、よくある感じの問題だけど、
(3)で不等式があるのが珍しい感じです。
図を描くと、こうです。

PとQがy軸対称なので、Cもy軸対称。よってb=0
となりそうだけど、これは証明した方が無難ですね。
(3)は、求めたAの式が複雑になるので、どうやって示すか?
その選択が大事なところです。
続きを読む




