2017年01月26日
2017日本数学オリンピック予選(問題9)
こんにちは。
JMO予選の第9問。これは難問。

並べ替え自体が2017!通りあるので、答はもっと大きな数になる。
なので「!」とか使って表すことになります。
F(σ)のすべての和
これでも十分難しいのだけど、さらに4乗せよとのこと。
次の等式を使うので、あらかじめ書き出しておきます。
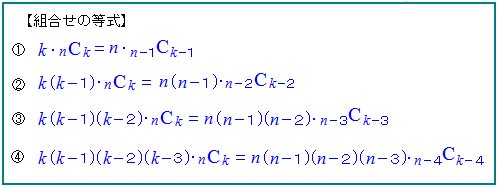
それぞれ、左辺のCを!を使って書き換えれば右辺になります。
続きを読む
JMO予選の第9問。これは難問。

並べ替え自体が2017!通りあるので、答はもっと大きな数になる。
なので「!」とか使って表すことになります。
F(σ)のすべての和
これでも十分難しいのだけど、さらに4乗せよとのこと。
次の等式を使うので、あらかじめ書き出しておきます。
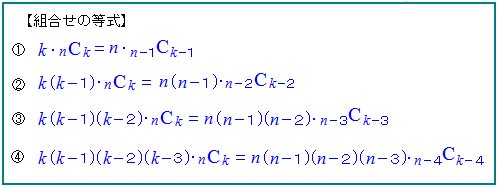
それぞれ、左辺のCを!を使って書き換えれば右辺になります。
続きを読む
2017年01月25日
2017日本数学オリンピック予選(問題8)
こんにちは。
引き続きJMO予選。
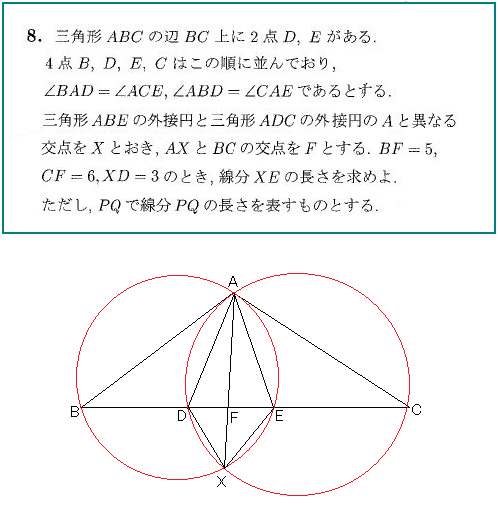
幾何の問題は理詰めで解けない。
図の中の何かカギとなるものに気付けないと一生解けないですね。
この問題、BXとCXをなにげに引いてみたら、解が浮かんだ。
幾何の問はこういう偶然が多いです・・。
続きを読む
引き続きJMO予選。

幾何の問題は理詰めで解けない。
図の中の何かカギとなるものに気付けないと一生解けないですね。
この問題、BXとCXをなにげに引いてみたら、解が浮かんだ。
幾何の問はこういう偶然が多いです・・。
続きを読む
2017年01月24日
2017日本数学オリンピック予選(問題7)
こんにちは。
私立大学の入試がそろそろ始まる頃ですね。
このJMO、のんびり解いている時間が無くなりそうだ。

例えば1、2、・・・、14の14個の数で考えてみると、次が「よい並べ替え」の1つの例になる。

5の倍数と7の倍数を順にチェンジすれば、倍数の関係は保たれるし、
他の数は動いてないのでOKのままです。
この場合、5の倍数と7の倍数の個数が同じなのでうまくいったことになる。
探し方は見えたのだけど、いざ解答を作るとなるとよくわからない・・。
続きを読む
私立大学の入試がそろそろ始まる頃ですね。
このJMO、のんびり解いている時間が無くなりそうだ。

例えば1、2、・・・、14の14個の数で考えてみると、次が「よい並べ替え」の1つの例になる。

5の倍数と7の倍数を順にチェンジすれば、倍数の関係は保たれるし、
他の数は動いてないのでOKのままです。
この場合、5の倍数と7の倍数の個数が同じなのでうまくいったことになる。
探し方は見えたのだけど、いざ解答を作るとなるとよくわからない・・。
続きを読む
2017年01月22日
2017日本数学オリンピック予選(問題6)
こんにちは。
漸化式が与えられていて、144番目を求めるだけの問題。
しかし漸化式が変な形をしていて、一般項などたぶんわからない。

こういう問は、項をいくつか求めてパターンを見つけることですね。
13が基準になっていそうなので、13ごとに分けて表を埋めていく。

第66項まではこのようになって、1の列がうまい具合に2の累乗になっている。
おまけに144項は1の列にあるので、
1の列には、2の累乗がずっと続く ・・・★
これが証明できればOKで、答が簡単に出る。
しかし証明ができなくてそれどころか、★を仮定すると矛盾が生じてしまう。
これは背理法の原理で、★が誤りだということが証明されたことになる。
それほど甘くないですね・・。
なので方針を変えた。
続きを読む
漸化式が与えられていて、144番目を求めるだけの問題。
しかし漸化式が変な形をしていて、一般項などたぶんわからない。

こういう問は、項をいくつか求めてパターンを見つけることですね。
13が基準になっていそうなので、13ごとに分けて表を埋めていく。

第66項まではこのようになって、1の列がうまい具合に2の累乗になっている。
おまけに144項は1の列にあるので、
1の列には、2の累乗がずっと続く ・・・★
これが証明できればOKで、答が簡単に出る。
しかし証明ができなくてそれどころか、★を仮定すると矛盾が生じてしまう。
これは背理法の原理で、★が誤りだということが証明されたことになる。
それほど甘くないですね・・。
なので方針を変えた。
続きを読む
2017年01月20日
2017年01月19日
2017日本数学オリンピック予選(問題4)
こんにちは。
授業はじめに行う3分間テスト。易しい計算ドリルなのだけど、
ビリの生徒にはペナルティとまで行かないが、机上に目印が置かれる。

その名を、「不幸を呼ぶ金ダルマ」
テストは優劣を決めるのが目的でなく、理解と意欲をUPさせるものであるべき。
なので見回りながら、ヒントをあげたり声援を送ったりしている。
「先生、静かにして!!」
私うるさいようですね・・。
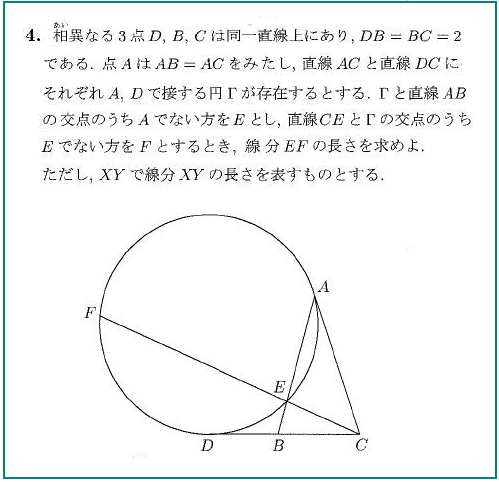
弦の長さと言えば、「方べき」ですね。
もうこれしかないくらいベタな問です。
続きを読む
授業はじめに行う3分間テスト。易しい計算ドリルなのだけど、
ビリの生徒にはペナルティとまで行かないが、机上に目印が置かれる。

その名を、「不幸を呼ぶ金ダルマ」
テストは優劣を決めるのが目的でなく、理解と意欲をUPさせるものであるべき。
なので見回りながら、ヒントをあげたり声援を送ったりしている。
「先生、静かにして!!」
私うるさいようですね・・。

弦の長さと言えば、「方べき」ですね。
もうこれしかないくらいベタな問です。
続きを読む
2017年01月18日
2017日本数学オリンピック予選(問題3)
こんにちは。
引き続きJMO予選。
第3問は、長方形の面積を求めるだけの問だった。

とりあえず数たちを文字で置き換えてみよう、という発想が大切で、
面白い問ですね。置き換えたのち因数分解ができるとありがたい。
そういう願いを持って計算をするといいです。
続きを読む
引き続きJMO予選。
第3問は、長方形の面積を求めるだけの問だった。

とりあえず数たちを文字で置き換えてみよう、という発想が大切で、
面白い問ですね。置き換えたのち因数分解ができるとありがたい。
そういう願いを持って計算をするといいです。
続きを読む
2017年01月18日
2017日本数学オリンピック予選(問題2)
こんにちは。
先週おこなわれたJMO予選。
第2問は場合の数の問題。

29!・・・・・・1から29までの自然数の積
互いに素・・・公約数が1だけになる自然数の組のこと
aとbの値が大きすぎて直接わからないのだけど、わからなくても解ける。
これは思考力を試す良問かと思う。
続きを読む
先週おこなわれたJMO予選。
第2問は場合の数の問題。

29!・・・・・・1から29までの自然数の積
互いに素・・・公約数が1だけになる自然数の組のこと
aとbの値が大きすぎて直接わからないのだけど、わからなくても解ける。
これは思考力を試す良問かと思う。
続きを読む
2017年01月17日
2017日本数学オリンピック予選(問題1)
こんにちは。
毎年1月におこなわれるJMO予選。
今年こそ解くのをやめよう、と毎年思っている。なぜかと言うと、
解けなくてずっと悩み続け、仕事に支障をきたすから。
今年も仕事中断で、取りかかってしまった・・。

四角形は凸でなく凹んだ形になりますね。
補助線を引けば自然に求まる。
続きを読む
毎年1月におこなわれるJMO予選。
今年こそ解くのをやめよう、と毎年思っている。なぜかと言うと、
解けなくてずっと悩み続け、仕事に支障をきたすから。
今年も仕事中断で、取りかかってしまった・・。

四角形は凸でなく凹んだ形になりますね。
補助線を引けば自然に求まる。
続きを読む
2016年12月31日
2016日本ジュニア数学オリンピック予選(問題8)
こんにちは。
JJMOの8番。
年内はこれで打ち止めですね。9番以降は解けたらUPします。

高校の数A「整数の性質」で習う合同式を知らないと、解くのはキツい。
数字は0~9までの10個あるので、全部使って10桁の37の倍数が作れないか?
これを考えるのだけど、どうやって37の倍数を見つけるのかが難しい。
37×3=111
37×3×9=999
なので、ここからわかることは、
3桁のゾロ目は皆37の倍数。
1000=37×27+1だから、1000を37で割ると余りが1
これを手掛かりにするよりない。
続きを読む
JJMOの8番。
年内はこれで打ち止めですね。9番以降は解けたらUPします。

高校の数A「整数の性質」で習う合同式を知らないと、解くのはキツい。
数字は0~9までの10個あるので、全部使って10桁の37の倍数が作れないか?
これを考えるのだけど、どうやって37の倍数を見つけるのかが難しい。
37×3=111
37×3×9=999
なので、ここからわかることは、
3桁のゾロ目は皆37の倍数。
1000=37×27+1だから、1000を37で割ると余りが1
これを手掛かりにするよりない。
続きを読む
2016年12月29日
2016日本ジュニア数学オリンピック予選(問題7)
こんにちは。
JJMOの7番は円の問題。
これは一応中学の知識で解くことができる。
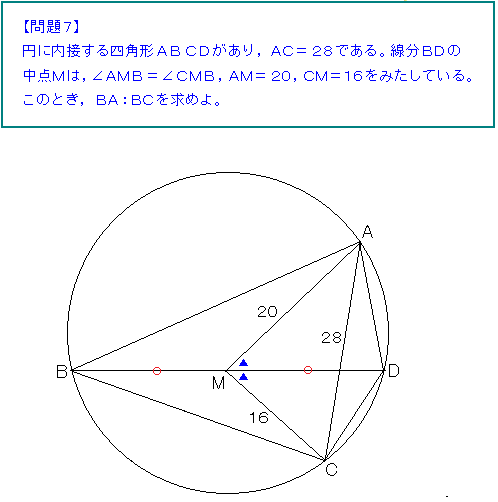
ABとBCの長さをそれぞれ求めようとすると一応答えが出るけど、
2重根号になる。こういう場合、その解き方は大体本解ではない。
AB:BCを求めるのだから、この比が三角形の相似比にならないか?
こう考えるのが筋ですな。あと、
折れ線はまっすぐ伸ばせ!!
中線は反転させよ!!!
こういう格言があって、これが役に立った感。
続きを読む
JJMOの7番は円の問題。
これは一応中学の知識で解くことができる。

ABとBCの長さをそれぞれ求めようとすると一応答えが出るけど、
2重根号になる。こういう場合、その解き方は大体本解ではない。
AB:BCを求めるのだから、この比が三角形の相似比にならないか?
こう考えるのが筋ですな。あと、
折れ線はまっすぐ伸ばせ!!
中線は反転させよ!!!
こういう格言があって、これが役に立った感。
続きを読む
2016年12月28日
2016日本ジュニア数学オリンピック予選(問題6)
こんにちは。
JJMOの6番は整数解の問。

大学入試に出てもおかしくない問題。式が複雑なのだけど、例えば

これなら左辺が因数分解できるので、何とか解けそうだとわかる。
なので、この形に持っていくことを目指します。
続きを読む
JJMOの6番は整数解の問。

大学入試に出てもおかしくない問題。式が複雑なのだけど、例えば

これなら左辺が因数分解できるので、何とか解けそうだとわかる。
なので、この形に持っていくことを目指します。
続きを読む
2016年12月26日
2016日本ジュニア数学オリンピック予選(問題5)
こんにちは。
中学の図形の問題。次のxはいくつか?
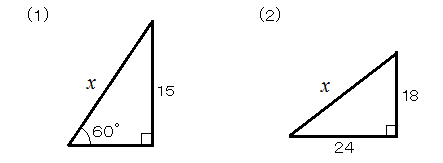
これは「三平方の定理」を使って普通次のように解く。

しかし(1)はともかく、(2)は数が大きくなるのでミスしやすい。
なので、次のように解くといいです。

(1)は、どの辺を何倍するか何で割るか?これを覚えておくと早いです。
(2)は、相似で小さい三角形を描くのが手間だけど、後の計算がラクになる。
JJMO予選の続き。
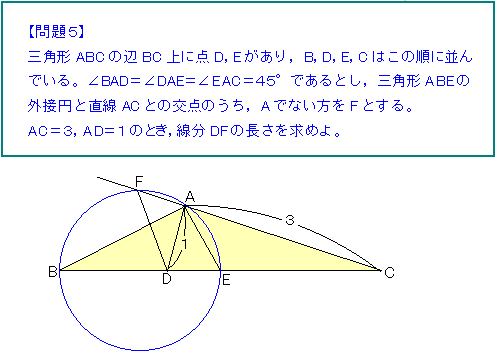
△ADFが直角三角形だから、AFがわかればDFも求まる。
この図は「方べき」の典型ですね。DE、CE、BEを求めて「方べき」にぶち込めばよろし。
続きを読む
中学の図形の問題。次のxはいくつか?

これは「三平方の定理」を使って普通次のように解く。

しかし(1)はともかく、(2)は数が大きくなるのでミスしやすい。
なので、次のように解くといいです。

(1)は、どの辺を何倍するか何で割るか?これを覚えておくと早いです。
(2)は、相似で小さい三角形を描くのが手間だけど、後の計算がラクになる。
JJMO予選の続き。

△ADFが直角三角形だから、AFがわかればDFも求まる。
この図は「方べき」の典型ですね。DE、CE、BEを求めて「方べき」にぶち込めばよろし。
続きを読む
2016年12月25日
2016日本ジュニア数学オリンピック予選(問題4)
こんにちは。
3連休、久々オフだった。
JJMO日本ジュニア数学オリンピックは出場資格が中学生以下だけど、
問題を見る限り、高校で習う範囲もかなり含まれていてキツイですね。
今日何問か解いてみたけど、後半かなり激ムズだった。
次は中学レベルの文章問題で、思考力を試す良問かと思う。

こういう問題のように個数が多いとき、いきなりxとおいて解こうとすると、
正論を見失う。まずは少ない場合で調べてみるといいです。

上の場合、条件を満たす人はユキ、ミキの2人ですが、アキとケンの
みかんをヒロシに移せば、この2人も条件を満たすことになる。
なので、ここでのヒロシのような負け役を設定しておくといい。
こういう考察をしたあと、文字xを使って数量を表していきます。
続きを読む
3連休、久々オフだった。
JJMO日本ジュニア数学オリンピックは出場資格が中学生以下だけど、
問題を見る限り、高校で習う範囲もかなり含まれていてキツイですね。
今日何問か解いてみたけど、後半かなり激ムズだった。
次は中学レベルの文章問題で、思考力を試す良問かと思う。

こういう問題のように個数が多いとき、いきなりxとおいて解こうとすると、
正論を見失う。まずは少ない場合で調べてみるといいです。

上の場合、条件を満たす人はユキ、ミキの2人ですが、アキとケンの
みかんをヒロシに移せば、この2人も条件を満たすことになる。
なので、ここでのヒロシのような負け役を設定しておくといい。
こういう考察をしたあと、文字xを使って数量を表していきます。
続きを読む
2016年02月20日
2016日本数学オリンピック予選(問題8)
こんにちは。
辺の長さや角度を求める図形の問題で、何か線を1本引くとうまく解ける
というミラクルな解法があったりするけど、どういう根拠で引くのか?
わからんですな・・。
これは経験、でしょうね。
JMO予選第8問。

図がシンプルである分、却って難しい。

三角形の内接円が描かれているときに考えることと言えば、
(1)方べきの定理(接線バージョン)が使えないか?
(2)△ABCの面積=(3辺の和)×(半径)÷2が使えないか?
(3)(中心と接点を結んだ線分)⊥(辺)が使えないか?
(4)直径を斜辺にする直角三角形が役に立たないか?
このあたりですかね。
xとyを設定して、ヘロンの公式や余弦定理にぶち込むのは芸が無い。
続きを読む
辺の長さや角度を求める図形の問題で、何か線を1本引くとうまく解ける
というミラクルな解法があったりするけど、どういう根拠で引くのか?
わからんですな・・。
これは経験、でしょうね。
JMO予選第8問。

図がシンプルである分、却って難しい。

三角形の内接円が描かれているときに考えることと言えば、
(1)方べきの定理(接線バージョン)が使えないか?
(2)△ABCの面積=(3辺の和)×(半径)÷2が使えないか?
(3)(中心と接点を結んだ線分)⊥(辺)が使えないか?
(4)直径を斜辺にする直角三角形が役に立たないか?
このあたりですかね。
xとyを設定して、ヘロンの公式や余弦定理にぶち込むのは芸が無い。
続きを読む
2016年02月17日
2016日本数学オリンピック予選(問題7)
こんにちは。
いよいよ来週から国立大の2次試験ですね。
次の恒等式は知らなくてもたぶん困らないけど、

うまく活用すると最大・最小に威力を発揮しますよ。
JMO予選の7問目。あと何問解けるかどうか・・?

シンプルで美しい。こういう対称式の問題で意識することは、
対称性を崩さない
1つの文字を消すとか、条件式を展開して引くとか・・
そういうセンスの無いことはやめよう。
続きを読む
いよいよ来週から国立大の2次試験ですね。
次の恒等式は知らなくてもたぶん困らないけど、

うまく活用すると最大・最小に威力を発揮しますよ。
JMO予選の7問目。あと何問解けるかどうか・・?

シンプルで美しい。こういう対称式の問題で意識することは、
対称性を崩さない
1つの文字を消すとか、条件式を展開して引くとか・・
そういうセンスの無いことはやめよう。
続きを読む
2016年02月13日
2016日本数学オリンピック予選(問題6)
こんにちは。
数学の問題が解けないとき、どんな思考をすればよいか?
【解けないときの思考法】
1)問題文を、もう一度しっかり読む。
2)具体例を調べて、手掛かりをつかむ。
3)解けない原因は何か、これを探る。
4)知っている解法を、こじつけてみる。
私はこんな感じですかね。
解けなくてすぐに答えを見る生徒はいるけど、それでは力がつかない。
この4ヶ条だけは実践してみてほしいです。
JMO予選の第6問。

上の4ヶ条のうちの2)で、1以上4以下の整数で試してみた。

得点の平均は、(16+4+0+0+4+16)÷6=20/3
個数が少なすぎて手掛かりが無いけど、得点が左右対称になっている。
これと同じ方法で200個を扱うのはとても不可能。何かうまい手が必要になる。
・丸印の和をXとして、得点をXで表すのはどうか?
・数が大きすぎるので、小さく、なおかつ対称形で扱えないか?
・得点を足していくのでなく、数ごとに足すという考えはどうか?
・和の2乗の公式(a+b+・・・+z)^2を、うまく利用できないか?
これらが4ヶ条の4)に当たるのだけど、果たして方針が正しいのかどうか・・。
続きを読む
数学の問題が解けないとき、どんな思考をすればよいか?
【解けないときの思考法】
1)問題文を、もう一度しっかり読む。
2)具体例を調べて、手掛かりをつかむ。
3)解けない原因は何か、これを探る。
4)知っている解法を、こじつけてみる。
私はこんな感じですかね。
解けなくてすぐに答えを見る生徒はいるけど、それでは力がつかない。
この4ヶ条だけは実践してみてほしいです。
JMO予選の第6問。

上の4ヶ条のうちの2)で、1以上4以下の整数で試してみた。

得点の平均は、(16+4+0+0+4+16)÷6=20/3
個数が少なすぎて手掛かりが無いけど、得点が左右対称になっている。
これと同じ方法で200個を扱うのはとても不可能。何かうまい手が必要になる。
・丸印の和をXとして、得点をXで表すのはどうか?
・数が大きすぎるので、小さく、なおかつ対称形で扱えないか?
・得点を足していくのでなく、数ごとに足すという考えはどうか?
・和の2乗の公式(a+b+・・・+z)^2を、うまく利用できないか?
これらが4ヶ条の4)に当たるのだけど、果たして方針が正しいのかどうか・・。
続きを読む
2016年02月12日
2016日本数学オリンピック予選(問題5)
こんにちは。
朝晩冷えますね。
受験シーズンのおり、なかなか記事を作る時間が取れず・・。
JMOの第5問です。


△ABCと△APDが二等辺三角形になって、しかも相似なる。
ここまでは見抜けるでしょうけど、そのあとが気づきにくい。
面積が出せないときは、全体から余分を引く
この法則で行くといいです。
続きを読む
朝晩冷えますね。
受験シーズンのおり、なかなか記事を作る時間が取れず・・。
JMOの第5問です。


△ABCと△APDが二等辺三角形になって、しかも相似なる。
ここまでは見抜けるでしょうけど、そのあとが気づきにくい。
面積が出せないときは、全体から余分を引く
この法則で行くといいです。
続きを読む
2016年01月30日
2016日本数学オリンピック予選(問題4)
こんにちは。
センター試験が終わり、国立2次と私立一般に向けてスパートですね。
数学Ⅰに「データの分析」という分野があって、センターでは必須になっている。
この分野の問いを2問作ってほしいと言われ、今週ずっと考えていた。

この相関図は相関係数が0.7になるように、苦労して作った・・。
この仕事もう勘弁ですね・・。
JMOの第4問です。

内側の1個と外側の4個に分けてカウントし、掛け合わせればいいです。
答えを見ずに解いて行ったところ、2度ほど間違えた。
私はこの試験受からないですね・・。
続きを読む
センター試験が終わり、国立2次と私立一般に向けてスパートですね。
数学Ⅰに「データの分析」という分野があって、センターでは必須になっている。
この分野の問いを2問作ってほしいと言われ、今週ずっと考えていた。

この相関図は相関係数が0.7になるように、苦労して作った・・。
この仕事もう勘弁ですね・・。
JMOの第4問です。

内側の1個と外側の4個に分けてカウントし、掛け合わせればいいです。
答えを見ずに解いて行ったところ、2度ほど間違えた。
私はこの試験受からないですね・・。
続きを読む
2016年01月17日
2016日本数学オリンピック予選(問題3)
こんにちは。
センター試験終わりましたね。
早速、解かねば・・。
JMOはしばし休みです。

正確な図がうまく描けないが、こんな感じになる。
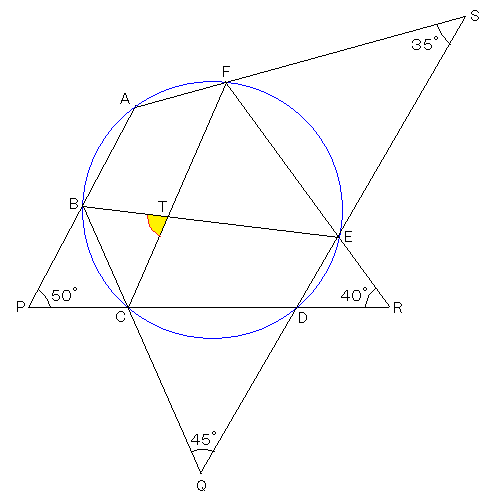
三角形の内角の和は180°
内接四角形の対角の和は180°
円周角の定理(=同じ弧に対する円周角は等しい)
この3つを使えば解けるはず。あとはどう補助線を引くかです。
続きを読む
センター試験終わりましたね。
早速、解かねば・・。
JMOはしばし休みです。

正確な図がうまく描けないが、こんな感じになる。

三角形の内角の和は180°
内接四角形の対角の和は180°
円周角の定理(=同じ弧に対する円周角は等しい)
この3つを使えば解けるはず。あとはどう補助線を引くかです。
続きを読む






