2024年09月21日
玉を取り出す確率。
こんにちは。
会社によくセールスが来るのだけど、
「珈琲の機械を置きませんか?」
という人が来た。
私は珈琲バカ。一日に何杯も飲むのだけど、
「ネルドリップが一番うまい」
と言ったら、その人ネルドリップを知らないと言う。

こういうやつです。知っててほしかったな。
今日は条件付き確率の問を1つ。

最近you tubeで観た問なのだけど、それは合計が10でなく文字のNだった。
その動画の解き方が何だかよくわからなかったな・・。
直感だと、次の3通りがありますね。
1)何回取り出しても五分五分なので、答えは50%
2)1回目が赤だから、赤が有利。答えは50%よりやや高い。
3)1回目が赤だから、赤が1個減って白が有利。答えは50%よりやや低い。
どれだと思います?
こういう直感も案外大事なことかと思う。
ではどう解くか?条件付き確率なので、教科書通りの設定です。
A:箱から1個取り出したらそれが赤玉である
B:箱から2個目を取り出したらそれが赤玉である
すると、こういう式になる。
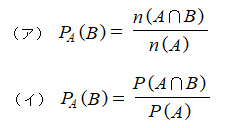
2つのうちやりやすい方を使えばいいけど、(ア)で行けるならそれがいいです。
これ、初期設定がわからないのでAもBも何通りか困ってしまいますね。
問の最後に書いた但し書きに合わせて11パターン全部を考えることになります。
会社によくセールスが来るのだけど、
「珈琲の機械を置きませんか?」
という人が来た。
私は珈琲バカ。一日に何杯も飲むのだけど、
「ネルドリップが一番うまい」
と言ったら、その人ネルドリップを知らないと言う。

こういうやつです。知っててほしかったな。
今日は条件付き確率の問を1つ。

最近you tubeで観た問なのだけど、それは合計が10でなく文字のNだった。
その動画の解き方が何だかよくわからなかったな・・。
直感だと、次の3通りがありますね。
1)何回取り出しても五分五分なので、答えは50%
2)1回目が赤だから、赤が有利。答えは50%よりやや高い。
3)1回目が赤だから、赤が1個減って白が有利。答えは50%よりやや低い。
どれだと思います?
こういう直感も案外大事なことかと思う。
ではどう解くか?条件付き確率なので、教科書通りの設定です。
A:箱から1個取り出したらそれが赤玉である
B:箱から2個目を取り出したらそれが赤玉である
すると、こういう式になる。
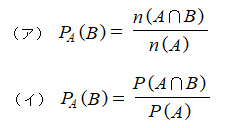
2つのうちやりやすい方を使えばいいけど、(ア)で行けるならそれがいいです。
これ、初期設定がわからないのでAもBも何通りか困ってしまいますね。
問の最後に書いた但し書きに合わせて11パターン全部を考えることになります。

(イ)を使うとどうなるのか?
まず、赤と白は対称と考えていいので、P(A)=1/2
あとはA∩Bだけど、これはどれかの箱から赤を2個取り出す確率になる。
これを計算すると、P(A∩B)=1/3 となり、答えが合います。
余力のある人は、全体の数をNにして解いてみてください。
結局同じ2/3になります。
また明日。
Posted by 三石 at 22:27│Comments(0)
│確率









