2018年09月24日
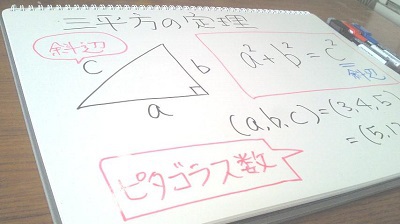
ピタゴラス数
こんにちは。
これはホワイトボードのスケッチブック版のようなもの。
黒板に板書する代わりに使おうと、買ってみた。
授業を通じて数学に対する意識や意欲を高めて欲しいと
つね思っていて、そういう授業を心がけては来た。
要は、学ぶことが楽しい、もっとできるようになりたい
こういう気持ちにさせること。
まだまだ、です・・。

ピタゴラス数はこちら。
この事実はよく知られているのだけど、自分で証明したことが無かった。
例えば、
(a、b、c)=(3、4、5) ⇒m=2、n=1とすればいい。
(a、b、c)=(5、12、13) ⇒m=3、n=2とすればいい。
しかしm=3、n=1とした場合、(a、b、c)=(8、6、10)となって、
全部偶数なので2で割ると、上の(3、4、5)と同じものになる。
m、nの取り方によっては最大公約数が1にならないことがある。
示したいことは、
最大公約数が1であるピタゴラス数のどんな組に対しても、
うまい自然数m、nをその都度見つけることによって、
ピタゴラス数をm2-n2、2mn、m2+n2という形で表すことができる。
ということです。
(注)wikipediaにはm-nが奇数とか、必要十分とか書いてますが、
そこまで言及しないことにします。証明が面倒なので。
これはホワイトボードのスケッチブック版のようなもの。

黒板に板書する代わりに使おうと、買ってみた。
授業を通じて数学に対する意識や意欲を高めて欲しいと
つね思っていて、そういう授業を心がけては来た。
要は、学ぶことが楽しい、もっとできるようになりたい
こういう気持ちにさせること。
まだまだ、です・・。

ピタゴラス数はこちら。
この事実はよく知られているのだけど、自分で証明したことが無かった。
例えば、
(a、b、c)=(3、4、5) ⇒m=2、n=1とすればいい。
(a、b、c)=(5、12、13) ⇒m=3、n=2とすればいい。
しかしm=3、n=1とした場合、(a、b、c)=(8、6、10)となって、
全部偶数なので2で割ると、上の(3、4、5)と同じものになる。
m、nの取り方によっては最大公約数が1にならないことがある。
示したいことは、
最大公約数が1であるピタゴラス数のどんな組に対しても、
うまい自然数m、nをその都度見つけることによって、
ピタゴラス数をm2-n2、2mn、m2+n2という形で表すことができる。
ということです。
(注)wikipediaにはm-nが奇数とか、必要十分とか書いてますが、
そこまで言及しないことにします。証明が面倒なので。

この結果、★のa、b、cに対するm、nの存在が言えます。
例えば(a、b、c)=(8、15、17)については、次の通り。

後から気づいたのだけど、a、bのうち偶数の方をbにしておけば、
(イ)の場合を排除できますね。お粗末だった・・。
いろいろと発見があって面白いものですね。
また明日。
Posted by 三石 at 16:19│Comments(0)
│等式