三石・数学塾

こんにちは。


３連休。ゆっくり休めた。
大学入学共通テストは次の土日ですか。
数学はどんな問が出るのでしょーか？
去年は評判が悪かったようです。良い問題を期待したいです。

ルート２のシリーズ、その３です。



ルート２が有理数であると仮定して、どこかで矛盾が起こることを示す。
という「背理法」で示すのが一般的なもので、こちら。


昔の記事はこちら。
その１
その２

これ以外に証明方法がないかどうか？
２つ発見しました。
まずは、教科書の証明と似ているけど若干違う次の方法。



分母を３以上に限定しておくことで、違った矛盾が起こります。
この方法だと、置き換えをして同じ形に持っていくという手間が省ける。

もう１つは、合同式を使ったものです。

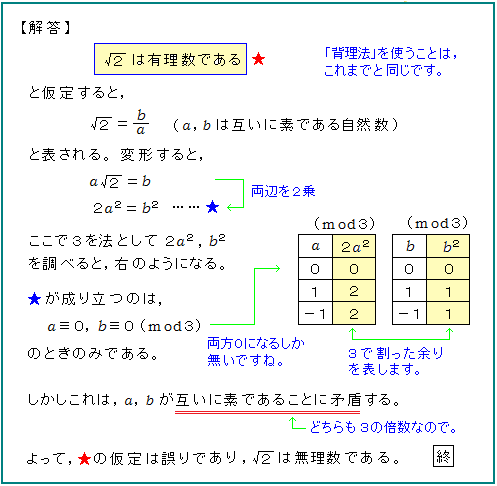
３を法にしてやってみたら、偶然うまく行きましたね。

定理や公式とか、これを証明させる問題はあまり入試で出ないのだけど、
これらを導く過程の中に有益な情報があると思うし、１つのことにいろいろな
アプローチの方法を知るのも、応用力を伸ばすことにつながると思う。

また明日。