2025年03月23日
2025早大・商(第1問の4)
こんにちは。
引き続き、早大商学部。

今日は(4)です。
難問だ。正9角形が馴染みが無い。60°の角度がどうやって作られるか?
ここをまず調べるしかないですね。
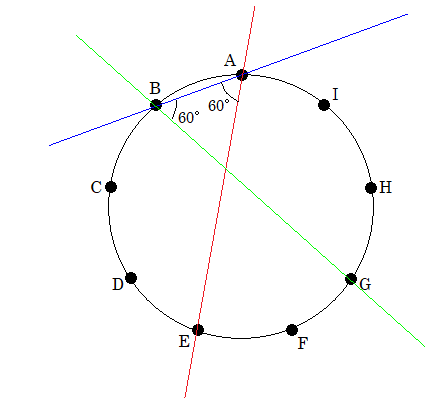
円を描いて、円周角を考えるといいです。
図のような赤、青、緑の線をひくと、正三角形ができます。
あとはこれらの直線を平行移動しても同じ60°の角ができる。
こんな感じで数えていきます。
続きを読む
引き続き、早大商学部。

今日は(4)です。
難問だ。正9角形が馴染みが無い。60°の角度がどうやって作られるか?
ここをまず調べるしかないですね。

円を描いて、円周角を考えるといいです。
図のような赤、青、緑の線をひくと、正三角形ができます。
あとはこれらの直線を平行移動しても同じ60°の角ができる。
こんな感じで数えていきます。
続きを読む
2025年03月22日
2025早大・商(第1問の3)
こんにちは。
天気の良い土曜日。
久々のオフだ。
休日引き続き、早大商学部。

今日は(3)です。
「等式を満たす」ということは、等式がxについての恒等式になるということです。
なのでm、nは任意でなく何か特定の数になるはずで、そこで両辺の次数を調べれば
m、nの条件が出て、値が決まるかな・・?
と、考えるところです。
続きを読む
天気の良い土曜日。
久々のオフだ。
休日引き続き、早大商学部。

今日は(3)です。
「等式を満たす」ということは、等式がxについての恒等式になるということです。
なのでm、nは任意でなく何か特定の数になるはずで、そこで両辺の次数を調べれば
m、nの条件が出て、値が決まるかな・・?
と、考えるところです。
続きを読む
2025年03月22日
2025早大・商(第1問の2)
こんにちは。
引き続き、早大商学部。

今日は(2)のみです。
3項間漸化式で、よくある形なのでそれほど難でない。
しかしa2でなくa2025が0というのが作為的ですな。
これ、0にしてくれているので案外ラクに解けます。
続きを読む
引き続き、早大商学部。

今日は(2)のみです。
3項間漸化式で、よくある形なのでそれほど難でない。
しかしa2でなくa2025が0というのが作為的ですな。
これ、0にしてくれているので案外ラクに解けます。
続きを読む
2025年03月20日
2025早大・商(第1問の1)
こんにちは。
もう3月か、早いですね。
いろんな入試が終わった、こういうとき仕事がカブるもので、
この時期は休みが無い。

行き付けの店にて。社長なので会社の経費で飲む。
これだけですな、社長やってて良いなと思うことは・・。
早稲田の商学部。
文系なのに数学が難しく、60点満点で平均が10点そこそこらしい。
どんな問が出てるのか見てみたら、なかなかだった。
面白いので解いてみますか。

大問1は小問集合4問だけど、どれも簡単でない。
今日は(1)のみです。
だいたい2つ式があるときはyを消してxの方程式を作るのだけど、
直接図を描くと、こうなるかな。
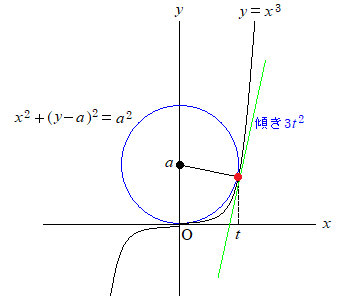
この図以外に共有点が2個になる場合が無いことを示す必要があるけど、
まあ細かいことは置いといて、式はこうなる。

この連立方程式を解けば一応答えは出るけど、あまりうまい解き方でない。
解答は、yを消す方法で。
続きを読む
もう3月か、早いですね。
いろんな入試が終わった、こういうとき仕事がカブるもので、
この時期は休みが無い。

行き付けの店にて。社長なので会社の経費で飲む。
これだけですな、社長やってて良いなと思うことは・・。
早稲田の商学部。
文系なのに数学が難しく、60点満点で平均が10点そこそこらしい。
どんな問が出てるのか見てみたら、なかなかだった。
面白いので解いてみますか。

大問1は小問集合4問だけど、どれも簡単でない。
今日は(1)のみです。
だいたい2つ式があるときはyを消してxの方程式を作るのだけど、
直接図を描くと、こうなるかな。

この図以外に共有点が2個になる場合が無いことを示す必要があるけど、
まあ細かいことは置いといて、式はこうなる。

この連立方程式を解けば一応答えは出るけど、あまりうまい解き方でない。
解答は、yを消す方法で。
続きを読む
2025年03月03日
2025東大・文系(第4問)
こんにちは。
引き続き東大文系。
最終の第4問は、面積の問題。

見た感じ対して難しくなさそうで、実際にそれほど難ではない。
しかし場合分けが多く、いちいち全部面積を求めていくと大変すぎる。
aを正として徐々に大きくしていくと、
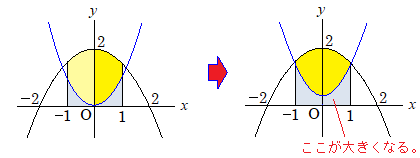
面積は小さくなっていくことがわかる。
aが負のときは絶対値のグラフが折り返されるのでややこしい。
-2から徐々に大きくしていくと、
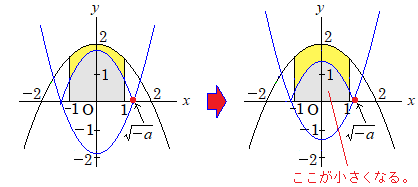
x軸との交点が±1の外にあれば、面積が大きくなっていくことがわかる。
これらを排除すれば、あとは-1≦a≦0のときを調べるだけでよくなる。
なかなか面倒な問だ。
続きを読む
引き続き東大文系。
最終の第4問は、面積の問題。

見た感じ対して難しくなさそうで、実際にそれほど難ではない。
しかし場合分けが多く、いちいち全部面積を求めていくと大変すぎる。
aを正として徐々に大きくしていくと、

面積は小さくなっていくことがわかる。
aが負のときは絶対値のグラフが折り返されるのでややこしい。
-2から徐々に大きくしていくと、

x軸との交点が±1の外にあれば、面積が大きくなっていくことがわかる。
これらを排除すれば、あとは-1≦a≦0のときを調べるだけでよくなる。
なかなか面倒な問だ。
続きを読む
2025年02月27日
2025東大・文系(第3問)
こんにちは。
引き続き東大文系。
第3問は確率の問題。これが一番難だった。

(2)は漸化式を作るタイプの問だろうと予測できるが、
どうやって式を立てればよいか?ここが相当ムズい。
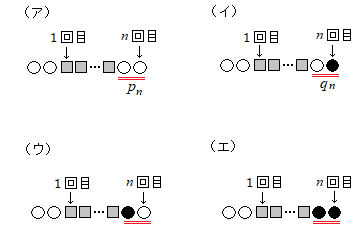
右から1番目と2番目の2個の玉のパターンはこの4つで、
アの確率pnとイの確率qnの和が(2)の答えになる。なので、
まずはpnとqnの関係式を作ろうかと考えるのが手順ですね。
続きを読む
引き続き東大文系。
第3問は確率の問題。これが一番難だった。

(2)は漸化式を作るタイプの問だろうと予測できるが、
どうやって式を立てればよいか?ここが相当ムズい。

右から1番目と2番目の2個の玉のパターンはこの4つで、
アの確率pnとイの確率qnの和が(2)の答えになる。なので、
まずはpnとqnの関係式を作ろうかと考えるのが手順ですね。
続きを読む
2025年02月27日
2025東大・文系(第2問)
こんにちは。
国立大の2次試験、昨日から始まりました。
引き続き東大文系、ゆうべ一応全部解けたけど、
やっぱどれも簡単でないですね。
第2問は図形の問題。

まずM、Nを中点、Oを外心として、小さめの円を描いてみる。
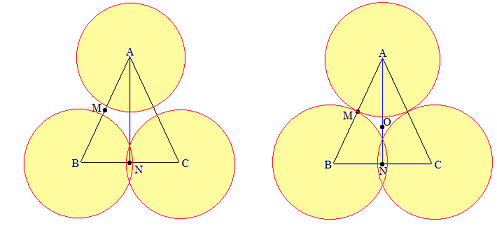
左図は、辺ABとACの一部がDrに含まれていない。
右図は、3辺がみなDrに含まれているが、Oの周りが含まれていない。
中点や外心を取ることに気付けるかどうか。
あと、鈍角三角形のときは外心が外に出るので解が違う。
なかなか面倒な問題だ・・。
続きを読む
国立大の2次試験、昨日から始まりました。
引き続き東大文系、ゆうべ一応全部解けたけど、
やっぱどれも簡単でないですね。
第2問は図形の問題。

まずM、Nを中点、Oを外心として、小さめの円を描いてみる。

左図は、辺ABとACの一部がDrに含まれていない。
右図は、3辺がみなDrに含まれているが、Oの周りが含まれていない。
中点や外心を取ることに気付けるかどうか。
あと、鈍角三角形のときは外心が外に出るので解が違う。
なかなか面倒な問題だ・・。
続きを読む
2025年02月25日
2025東大・文系(第1問)
こんにちは。
国立大の2次試験、本日から始まりました。
私はもう塾の先生でないので、受験生の心配は無い。
なので、のんびり解いていこうかと思います。
今年の東大。文系の方です。

(2)のほう、図をかくとこんな感じです。
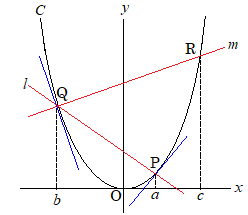
これ、PからQ、QからRと同じことをしているので、
b=(aの式)
を作ったら、c=(bの式)も同じ形になります。
これに気づけると二度手間が防げる。
しかし対象となるものが分数関数なので、どう処理するのか?
ここがややムズいです。
続きを読む
国立大の2次試験、本日から始まりました。
私はもう塾の先生でないので、受験生の心配は無い。
なので、のんびり解いていこうかと思います。
今年の東大。文系の方です。

(2)のほう、図をかくとこんな感じです。

これ、PからQ、QからRと同じことをしているので、
b=(aの式)
を作ったら、c=(bの式)も同じ形になります。
これに気づけると二度手間が防げる。
しかし対象となるものが分数関数なので、どう処理するのか?
ここがややムズいです。
続きを読む
2025年01月29日
2025日本数学オリンピック予選(問題5)
こんにちは。
行き付けの店に。

ボトルをキープして飲む。
こういうの若い頃は無かったな、金なかったし・・。
受験のシーズン。
そろそろ私の会社も忙しくなり、酒飲む時間も無くなりそうだ。
JMOの続きです。

図が入り組んでいて複雑ですな。どうすれば解けるのか?その発見が難しい。
形からして「メネラウスの定理」かな?と思ったが、求める比の形はその定理には出てこない。
でもひとまずは、BCとCDを文字で置いて、他の線分をその文字で表すことを考えます。
続きを読む
行き付けの店に。

ボトルをキープして飲む。
こういうの若い頃は無かったな、金なかったし・・。
受験のシーズン。
そろそろ私の会社も忙しくなり、酒飲む時間も無くなりそうだ。
JMOの続きです。

図が入り組んでいて複雑ですな。どうすれば解けるのか?その発見が難しい。
形からして「メネラウスの定理」かな?と思ったが、求める比の形はその定理には出てこない。
でもひとまずは、BCとCDを文字で置いて、他の線分をその文字で表すことを考えます。
続きを読む
2025年01月19日
2025日本数学オリンピック予選(問題4)
こんにちは。
大学入学共通テスト、終わったようですね。
数1A、数2Bともやや易化とのこと。
どこかにUPされ次第、解いていくことにします。
JMOの続き。

例えば、58と言う数。
58÷2=29あまり0
58÷3=19あまり1
58÷4=14あまり2
58÷5=11あまり3
58÷6=9 あまり4
となって、条件を満たします。
余りの方を先に決めて、それに見合うNを探す方法がよいです。
例えば58に2を足せば、2、3、4、5、6のどれでも割り切れる。
こういう都合のよい数を見つけると早いです。
続きを読む
大学入学共通テスト、終わったようですね。
数1A、数2Bともやや易化とのこと。
どこかにUPされ次第、解いていくことにします。
JMOの続き。

例えば、58と言う数。
58÷2=29あまり0
58÷3=19あまり1
58÷4=14あまり2
58÷5=11あまり3
58÷6=9 あまり4
となって、条件を満たします。
余りの方を先に決めて、それに見合うNを探す方法がよいです。
例えば58に2を足せば、2、3、4、5、6のどれでも割り切れる。
こういう都合のよい数を見つけると早いです。
続きを読む
2025年01月18日
2025日本数学オリンピック予選(問題3)
こんにちは。
引き続きJMO予選。

10×10のマス目

これに、次のピースを置くという問題。

パズルのようにいろんな並べ方がありそうで大変だな・・
と思ったが、どうも規則性があって割と簡単だった。
続きを読む
引き続きJMO予選。

10×10のマス目

これに、次のピースを置くという問題。

パズルのようにいろんな並べ方がありそうで大変だな・・
と思ったが、どうも規則性があって割と簡単だった。
続きを読む
2025年01月17日
2025日本数学オリンピック予選(問題1・2)
こんにちは。
明日から大学入学共通テストですね。
今年から数1Aの範囲が変わって、整数論の分野が消え、
確率、幾何が必須となってしまった。
幾何は勉強しにくい分野だし、点が取りにくい感じあるかな。
変わって、先週行われたJMO予選。
毎年解ける問だけ解いているけど、毎年沼にハマって、
仕事がおろそかになる。今日もそうだった。

全12問の中では易しいのだけど、どちらも数え上げなので、漏れが怖いです。
第1問では真ん中の数を先に決めるよりも、
「7」がどこに来るか?7と隣り合う数がどう入るか?を考える方がラクかな。
第2問は2025が平方数なので、2数の積が平方数になる条件を考えます。
続きを読む
明日から大学入学共通テストですね。
今年から数1Aの範囲が変わって、整数論の分野が消え、
確率、幾何が必須となってしまった。
幾何は勉強しにくい分野だし、点が取りにくい感じあるかな。
変わって、先週行われたJMO予選。
毎年解ける問だけ解いているけど、毎年沼にハマって、
仕事がおろそかになる。今日もそうだった。

全12問の中では易しいのだけど、どちらも数え上げなので、漏れが怖いです。
第1問では真ん中の数を先に決めるよりも、
「7」がどこに来るか?7と隣り合う数がどう入るか?を考える方がラクかな。
第2問は2025が平方数なので、2数の積が平方数になる条件を考えます。
続きを読む
2025年01月12日
2025共通テスト試作問題(数2BC)
こんにちは。
あと1週間ですね、共通テストが。
試作問題。こちら。
数2BCの第7問、これは数Cの問です。
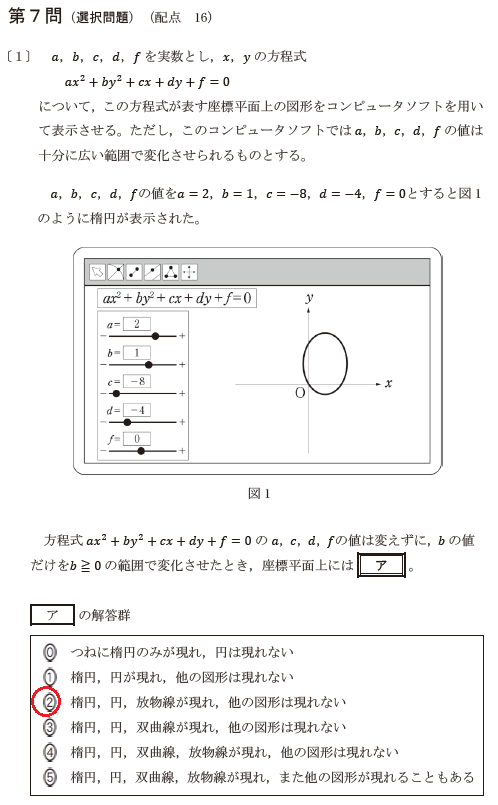
2次曲線はaとbの符号で形が決まる。それを知っていれば易しい。
続いて、〔2〕です。
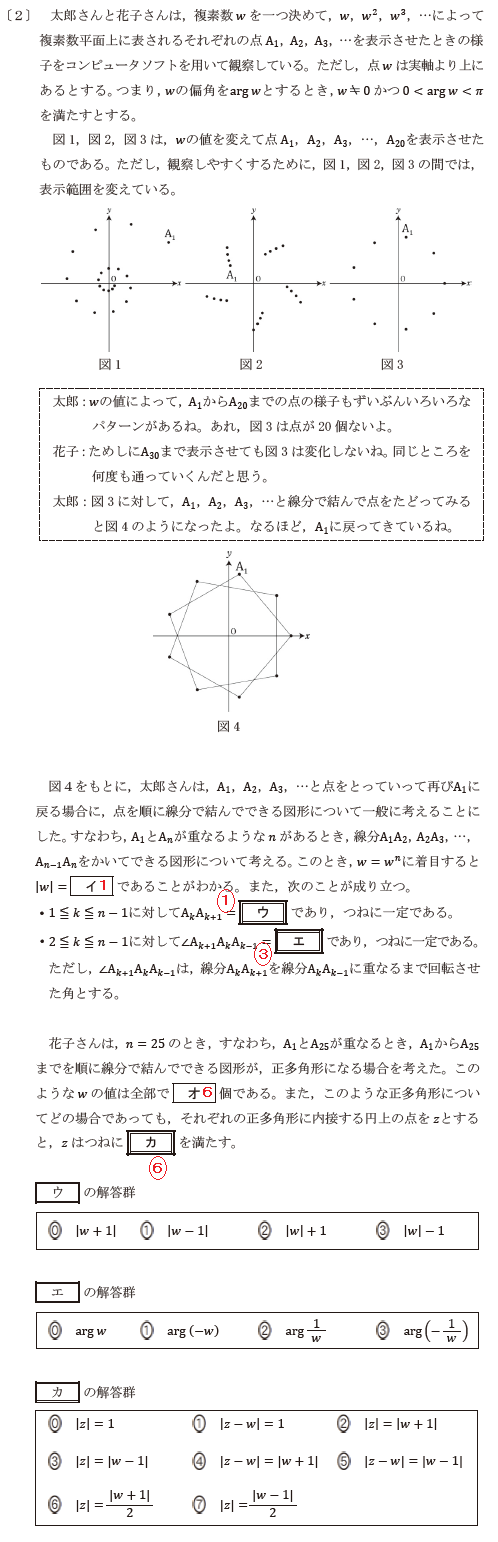
この問の図1と図2は、問題を解くのに全く必要としない。
こういう不要な情報をあえて入れてくるのも共通テストの特徴の1つかと思う。
続きを読む
あと1週間ですね、共通テストが。
試作問題。こちら。
数2BCの第7問、これは数Cの問です。

2次曲線はaとbの符号で形が決まる。それを知っていれば易しい。
続いて、〔2〕です。

この問の図1と図2は、問題を解くのに全く必要としない。
こういう不要な情報をあえて入れてくるのも共通テストの特徴の1つかと思う。
続きを読む
2025年01月11日
2025共通テスト試作問題(数1A)
こんにちは。
あと1週間ですね、共通テストが。
この試験の数学なのだけど、毎回解くたびに腹が立ってしまう。
文章がえらく長く、それが物語になっていて読解に苦労すること。
考え方を指定してそれに乗る必要があり、自由に発想できないこと。
答えが選択肢になるケースがあり、これを選ぶのがめんどいこと。
など。こういうことを分かったうえで根気よくしかもスピーディに
解く必要がありますね。もっとシンプルにできないものか・・?
数学の能力以外のとこで差がついてしまうのではと毎回思う。
試験問題はこういう感じになりますよ、というものがUPされていたので、
解いてみますか。こちら。
数1Aの第4問で、確率の問です。

ここまでは2021年の共通テスト1A第3問とほぼ同じです。
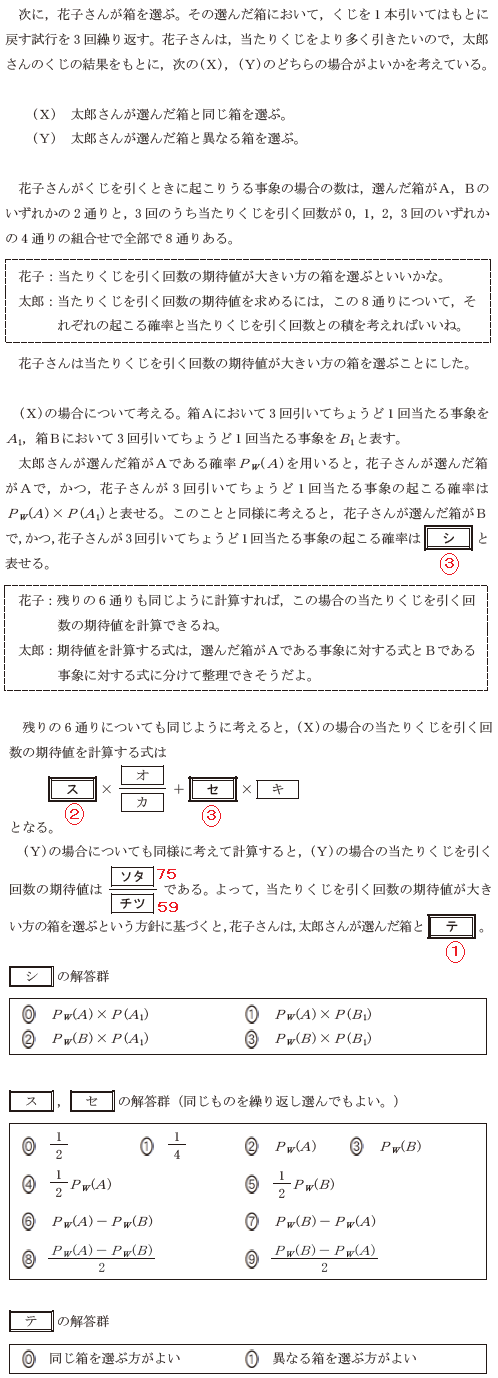
全4ページ。うんざりですな・・。
後半は文章量が多い割に設問が少ない。途中の会話文は、問題を解くうえで
ヒントになっているので読み飛ばさないほうがいい。
スセ以降が難しい。
一見、XとYのどちらを取っても期待値は変わらないように見えるけど、
太郎の試行で結果が1つ出ているので、それが花子の選択に影響しているというのが、
この問題の主旨となっている。厄介だ・・。
続きを読む
あと1週間ですね、共通テストが。
この試験の数学なのだけど、毎回解くたびに腹が立ってしまう。
文章がえらく長く、それが物語になっていて読解に苦労すること。
考え方を指定してそれに乗る必要があり、自由に発想できないこと。
答えが選択肢になるケースがあり、これを選ぶのがめんどいこと。
など。こういうことを分かったうえで根気よくしかもスピーディに
解く必要がありますね。もっとシンプルにできないものか・・?
数学の能力以外のとこで差がついてしまうのではと毎回思う。
試験問題はこういう感じになりますよ、というものがUPされていたので、
解いてみますか。こちら。
数1Aの第4問で、確率の問です。

ここまでは2021年の共通テスト1A第3問とほぼ同じです。

全4ページ。うんざりですな・・。
後半は文章量が多い割に設問が少ない。途中の会話文は、問題を解くうえで
ヒントになっているので読み飛ばさないほうがいい。
スセ以降が難しい。
一見、XとYのどちらを取っても期待値は変わらないように見えるけど、
太郎の試行で結果が1つ出ているので、それが花子の選択に影響しているというのが、
この問題の主旨となっている。厄介だ・・。
続きを読む
2025年01月02日
2025年元旦
令和7年。
明けましたね。
元旦の初詣は、毎年恒例の市内、元善光寺というお寺で、
そしていつもの絵馬です。

数学の問を神社に奉納していたという昔の文献を見て、それを真似した。
もうかれこれ20年近くやっていると思う。
自己満足なものですな。でも、これを見て数学に興味を持ってくれる学生が
いてくれると嬉しく思う。
続きを読む
明けましたね。
元旦の初詣は、毎年恒例の市内、元善光寺というお寺で、
そしていつもの絵馬です。

数学の問を神社に奉納していたという昔の文献を見て、それを真似した。
もうかれこれ20年近くやっていると思う。
自己満足なものですな。でも、これを見て数学に興味を持ってくれる学生が
いてくれると嬉しく思う。
続きを読む
2024年10月14日
豊作だった。
こんにちは。

3連休、実家の長野にいた。
田舎の良い点は、静かなこと。空気がうまいこと。
都会とは全然違うなと、感じた。
収穫前の実った穂を見て、こんな問を考えた。

全体を1とすれば、各自もらえる量がそれぞれ計算できるので、
それを比較すればOKです。
長男=0.1
次男=0.9×0.2=0.18
三男=(1-0.28)×0.3=0.216
・・・・・・・・・
しかしこういう方法でなく、漸化式っぽい解法を考えてみてください。
続きを読む

3連休、実家の長野にいた。
田舎の良い点は、静かなこと。空気がうまいこと。
都会とは全然違うなと、感じた。
収穫前の実った穂を見て、こんな問を考えた。

全体を1とすれば、各自もらえる量がそれぞれ計算できるので、
それを比較すればOKです。
長男=0.1
次男=0.9×0.2=0.18
三男=(1-0.28)×0.3=0.216
・・・・・・・・・
しかしこういう方法でなく、漸化式っぽい解法を考えてみてください。
続きを読む
2024年10月04日
組合せnCrの公式。
こんにちは。
残業中。ふう・・ひと息です。
このところやっと涼しくなってきた感。
東京の夏は暑いな。人込みと暑さ。これが困る・・
それ以外は便利で住みやすいのだけど。
数学の話。

期待値を計算していたらこういう式が出てきた。
これ、計算できるのだろうか?10個の項をそれぞれ書いて
計算するのでなく、1つのCの式にしたい。
k倍が邪魔なので、これを無くしてΣnCrという形にするというテクを使う。
組合せnCrの公式というと、次の(1)(2)は有名で、(3)は見かけないけど、
この(3)を使うとうまく行きます。
答 10×20C11

左辺か右辺を変形していけば証明できるけど、そうでなく、組合せの総数を
考えることで示せないか?それを考えてみました。
続きを読む
残業中。ふう・・ひと息です。
このところやっと涼しくなってきた感。
東京の夏は暑いな。人込みと暑さ。これが困る・・
それ以外は便利で住みやすいのだけど。
数学の話。

期待値を計算していたらこういう式が出てきた。
これ、計算できるのだろうか?10個の項をそれぞれ書いて
計算するのでなく、1つのCの式にしたい。
k倍が邪魔なので、これを無くしてΣnCrという形にするというテクを使う。
組合せnCrの公式というと、次の(1)(2)は有名で、(3)は見かけないけど、
この(3)を使うとうまく行きます。
答 10×20C11

左辺か右辺を変形していけば証明できるけど、そうでなく、組合せの総数を
考えることで示せないか?それを考えてみました。
続きを読む
2024年09月21日
玉を取り出す確率。
こんにちは。
会社によくセールスが来るのだけど、
「珈琲の機械を置きませんか?」
という人が来た。
私は珈琲バカ。一日に何杯も飲むのだけど、
「ネルドリップが一番うまい」
と言ったら、その人ネルドリップを知らないと言う。

こういうやつです。知っててほしかったな。
今日は条件付き確率の問を1つ。

最近you tubeで観た問なのだけど、それは合計が10でなく文字のNだった。
その動画の解き方が何だかよくわからなかったな・・。
直感だと、次の3通りがありますね。
1)何回取り出しても五分五分なので、答えは50%
2)1回目が赤だから、赤が有利。答えは50%よりやや高い。
3)1回目が赤だから、赤が1個減って白が有利。答えは50%よりやや低い。
どれだと思います?
こういう直感も案外大事なことかと思う。
ではどう解くか?条件付き確率なので、教科書通りの設定です。
A:箱から1個取り出したらそれが赤玉である
B:箱から2個目を取り出したらそれが赤玉である
すると、こういう式になる。
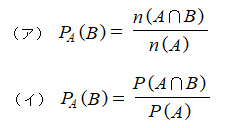
2つのうちやりやすい方を使えばいいけど、(ア)で行けるならそれがいいです。
これ、初期設定がわからないのでAもBも何通りか困ってしまいますね。
問の最後に書いた但し書きに合わせて11パターン全部を考えることになります。
続きを読む
会社によくセールスが来るのだけど、
「珈琲の機械を置きませんか?」
という人が来た。
私は珈琲バカ。一日に何杯も飲むのだけど、
「ネルドリップが一番うまい」
と言ったら、その人ネルドリップを知らないと言う。

こういうやつです。知っててほしかったな。
今日は条件付き確率の問を1つ。

最近you tubeで観た問なのだけど、それは合計が10でなく文字のNだった。
その動画の解き方が何だかよくわからなかったな・・。
直感だと、次の3通りがありますね。
1)何回取り出しても五分五分なので、答えは50%
2)1回目が赤だから、赤が有利。答えは50%よりやや高い。
3)1回目が赤だから、赤が1個減って白が有利。答えは50%よりやや低い。
どれだと思います?
こういう直感も案外大事なことかと思う。
ではどう解くか?条件付き確率なので、教科書通りの設定です。
A:箱から1個取り出したらそれが赤玉である
B:箱から2個目を取り出したらそれが赤玉である
すると、こういう式になる。
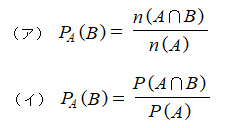
2つのうちやりやすい方を使えばいいけど、(ア)で行けるならそれがいいです。
これ、初期設定がわからないのでAもBも何通りか困ってしまいますね。
問の最後に書いた但し書きに合わせて11パターン全部を考えることになります。
続きを読む
2024年09月16日
待ち合わせ場所の指定。
こんにちは。
月イチの練習会の日。

ピアノとシンセが私、メンバーはギターとドラムの
ジャズトリオとなってます、一応。
ピアノはずっと独学で、通信教育とか受けたけど続かなかった。
やっぱ、なかなか上達しないな。数学と同じで・・。
東京、神奈川、茨城から、それぞれ3人が千葉のスタジオに集まる。
帰り道、こんな問を考えてました。

3軒の家は皆異なり、場所は定まっているけど、どのような配置かわからない。
しかし、家の配置や距離などに関係なく、答えは1つに決まります。
続きを読む
月イチの練習会の日。

ピアノとシンセが私、メンバーはギターとドラムの
ジャズトリオとなってます、一応。
ピアノはずっと独学で、通信教育とか受けたけど続かなかった。
やっぱ、なかなか上達しないな。数学と同じで・・。
東京、神奈川、茨城から、それぞれ3人が千葉のスタジオに集まる。
帰り道、こんな問を考えてました。

3軒の家は皆異なり、場所は定まっているけど、どのような配置かわからない。
しかし、家の配置や距離などに関係なく、答えは1つに決まります。
続きを読む
2024年09月11日
2024東京都教員教員採用試験(その2)
こんにちは。
9月半ば、まだ暑いですね。
友人が、借りていたカネ返すよと。

100万円になってる!
そういえば新札。1万円と千円は手に入ったけど、
五千円がなかなか回ってこないですね。まぁいいです。
東京都教員教員採用試験。こちら。
第3問です。

陰関数というもので、yについて解けば問2も問3も定積分の式が作れる。
なので、そう難しくないです。
続きを読む
9月半ば、まだ暑いですね。
友人が、借りていたカネ返すよと。

100万円になってる!
そういえば新札。1万円と千円は手に入ったけど、
五千円がなかなか回ってこないですね。まぁいいです。
東京都教員教員採用試験。こちら。
第3問です。

陰関数というもので、yについて解けば問2も問3も定積分の式が作れる。
なので、そう難しくないです。
続きを読む




