三石・数学塾

こんにちは。


都内から外に出られず、実家に帰ろうにも家族にNGされている。
私がもしコロナにかかっていたらマズい、と言うことで。
いつになったら安心して暮らせるのか・・。

私の会社は数学の会社。２年目に突入。

ウィルスの影響で売り上げが落ちた・・

こうならないようにせねば。
いまも仕事中だけど、ちょっと一息。


ずいぶん前の記事ですが、ルート２のシリーズ
その１　
その２　
その３　
その４　

その５は、
面積が２の長方形を徐々に正方形に近づけていく
という方法を考えました。



縦横の平均を次の長方形の縦にしていくと、だんだん正方形に近くなっていくので、
その1辺の長さが√２に近づいていくはずです。



縦の長さは、２、３/２、１７/１２、・・・のように減少します。
これが最後は√２に行くことを示せばOK。

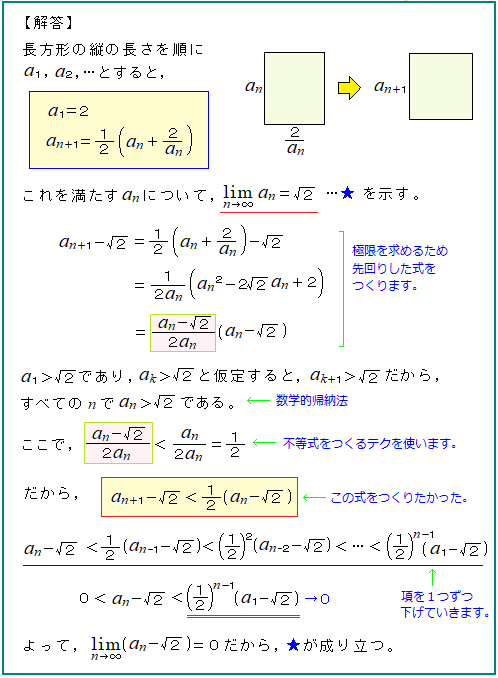
解けない漸化式から極限を求める問の典型的なもので、
偏差値にして５５を超える壁のような問かもしれない。

また明日。