2022年09月10日
垂線と垂心の関係とは?
こんにちは。
更新が途絶えておりました。多忙につき・・。
本を読むのに最近はもっぱら電子書籍なのだけど、
やっぱ紙の本を手に取って読むほうが私は良いかな。
何となく活字が頭に入って残る、というか。

いつもは数学書ばかりなのだけど、たまに随筆、文学系、歴史系も読む。
学生の頃、歴史は全く興味が無かった。けど、昔の人が考えてきたことや
失敗してきたことは、別な形で現代に活かせるものだと、思うようになった。
より良く生きるためのヒントがそこにある。そう思うわけです。
次は、昔の人が発見した、結構面白い事実です。
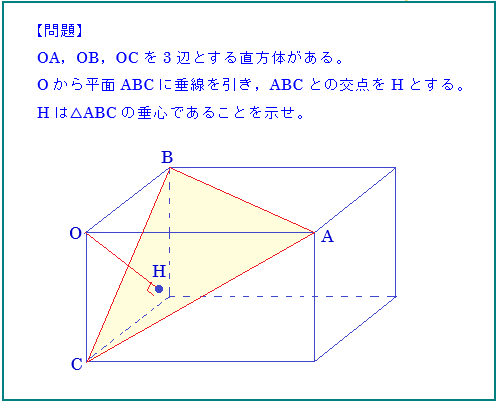
シンプルなのだけど、見た目、自明とは言いがたいですね。
どうやって証明するのか?それにはいくつか手があるけど、
策1 幾何だけで示す
策2 ベクトルの内積を使う
策3 座標空間に置く
1つの問題をいろんな方法で解くことは、学力向上の良い練習になるし、
そういうことができるような問題が、良問と言われるものかと思う。
更新が途絶えておりました。多忙につき・・。
本を読むのに最近はもっぱら電子書籍なのだけど、
やっぱ紙の本を手に取って読むほうが私は良いかな。
何となく活字が頭に入って残る、というか。

いつもは数学書ばかりなのだけど、たまに随筆、文学系、歴史系も読む。
学生の頃、歴史は全く興味が無かった。けど、昔の人が考えてきたことや
失敗してきたことは、別な形で現代に活かせるものだと、思うようになった。
より良く生きるためのヒントがそこにある。そう思うわけです。
次は、昔の人が発見した、結構面白い事実です。

シンプルなのだけど、見た目、自明とは言いがたいですね。
どうやって証明するのか?それにはいくつか手があるけど、
策1 幾何だけで示す
策2 ベクトルの内積を使う
策3 座標空間に置く
1つの問題をいろんな方法で解くことは、学力向上の良い練習になるし、
そういうことができるような問題が、良問と言われるものかと思う。
まずは策1。

「三垂線の定理」というものの応用、という感じ。途中、次の2つを使った。
1)直線L⊥平面Sならば、S上のどの直線もLに垂直。
2)直線Lが、平面S上の平行でない2直線と垂直ならば、L⊥S
わかりにくいっすね、文章にすると。
策2はこちら。

垂直とベクトルは相性がいい。
とりあえずベクトルの内積を作っていけば何とかなります。
策3は、暇があったらUPします。
また明日。

「三垂線の定理」というものの応用、という感じ。途中、次の2つを使った。
1)直線L⊥平面Sならば、S上のどの直線もLに垂直。
2)直線Lが、平面S上の平行でない2直線と垂直ならば、L⊥S
わかりにくいっすね、文章にすると。
策2はこちら。

垂直とベクトルは相性がいい。
とりあえずベクトルの内積を作っていけば何とかなります。
策3は、暇があったらUPします。
また明日。
Posted by 三石 at 04:39│Comments(0)
│幾何









