2020年01月01日
２０２０年元旦。
こんにちは。
２０２０年を迎えました。
今年も大都会の東京で、小さな会社を営む。
数学を学ぶ中高生に、よい物を届けたい。
という気持ちで仕事に励んでいるけど、
採算が合うようやりくりすること、簡単でない。
まあ頑張るしかないか。
初詣は、飯田市内の「元善光寺」。
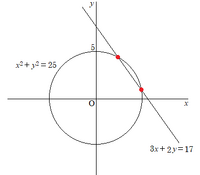
毎年恒例、絵馬を飾るのだけど、今年はこちら。
満たすa,bが無いかもしれないけど、
探してみたらありました。
２０２０年を迎えました。
今年も大都会の東京で、小さな会社を営む。
数学を学ぶ中高生に、よい物を届けたい。
という気持ちで仕事に励んでいるけど、
採算が合うようやりくりすること、簡単でない。
まあ頑張るしかないか。
初詣は、飯田市内の「元善光寺」。
毎年恒例、絵馬を飾るのだけど、今年はこちら。
満たすa,bが無いかもしれないけど、
探してみたらありました。
工夫した割に、大してうまくなかったですね。
解答を悩んでいたところ、息子がPCで即座に解を見つけてしまった・・。
味気ないものですな、これも時代か・・。
皆様、本年もよろしくお付き合いください。
また明日。
Posted by 三石 at 12:13│Comments(3)
│等式
この記事へのコメント
こんにちは！毎年問題を楽しく拝見させていただいています。
自分も初詣の際に説かせていただきました。
a'^2 +b'^2 = 505にするまでは同じだったのですが、自分はそこから5を法として考えて、題意を満たすには(a', b')≡(0, 0), (±1, ±2), (±2, ±1)のいずれかで表されることに注目して、そこからまず(0, 0)のパターンがないことを確認してから、a'≡±1となるような22以下の値をただひたすらに代入するという解き方で解かせていただきました。(16, 42)は出たのですが、505 - 361をミスって(24, 38)が出なかったのがやるせないです…。
自分も三石さんに憧れ、稚拙ながら問題を作らせていただいたので、お時間があったら解いていただけると嬉しいです。
p, q, rは素数とする。
p^2 + q^2 + 9r = 2020となるような(p, q, r )の組をすべて求めよ。
自分も初詣の際に説かせていただきました。
a'^2 +b'^2 = 505にするまでは同じだったのですが、自分はそこから5を法として考えて、題意を満たすには(a', b')≡(0, 0), (±1, ±2), (±2, ±1)のいずれかで表されることに注目して、そこからまず(0, 0)のパターンがないことを確認してから、a'≡±1となるような22以下の値をただひたすらに代入するという解き方で解かせていただきました。(16, 42)は出たのですが、505 - 361をミスって(24, 38)が出なかったのがやるせないです…。
自分も三石さんに憧れ、稚拙ながら問題を作らせていただいたので、お時間があったら解いていただけると嬉しいです。
p, q, rは素数とする。
p^2 + q^2 + 9r = 2020となるような(p, q, r )の組をすべて求めよ。
Posted by かまぼこ at 2020年01月01日 16:59
かまぼこさん
コメントありがとうございます。
5を法にするのはうまいですね。
問の答えは
（2,3,223),(3,2,223)
これ以外に無いような・・
コメントありがとうございます。
5を法にするのはうまいですね。
問の答えは
（2,3,223),(3,2,223)
これ以外に無いような・・
Posted by 三石
at 2020年01月03日 00:26
at 2020年01月03日 00:26返信ありがとうございます。
わざわざ解いていただいてありがとうございます！その通りです。
来年も問題、楽しみにしています。
わざわざ解いていただいてありがとうございます！その通りです。
来年も問題、楽しみにしています。
Posted by かまぼこさん at 2020年01月12日 19:11
