2019年08月11日
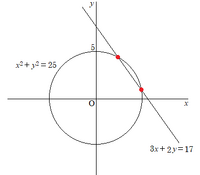
余弦定理の証明法。
こんにちは。
毎日暑いですね。
こちらは自作の、高3夏休み課題帳。

入試数学演習ⅠAⅡB/使用上の注意
1)解けなくてもすぐに答えを見ないこと。
2)この本の解答を、毎日読書すること。
3)1つの問題を、必ず2回は解くこと。
たった20問だけど、1問の中に多くの要素が含まれるよう問題を選んである。
冊子見本はこちら。塾は休業中。せっかく作ったのでどなたか活用ください。
数学の話。
定理や公式を証明することは、入試ではあまり出ないけど、証明をする過程の中に
結構重要な手法が隠れていることが、稀にある。

教科書を調べると、大体次のように垂線を引く。

これを見ると、三平方の定理と違うところが右辺の「-2cx」のところで、
bccosAはベクトルABとACの内積になることが発見できる。
また、逆にAHを求めたいときは、上の2行目の式をxについて解けばいい。
問1 Aが直角や鈍角の場合も成り立つことを確かめよ。
めんどくさくなったのか、こう書いてある教科書もありますね。
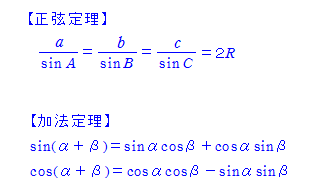
これらを使って余弦定理を導くことができるというので、考えてみた。
毎日暑いですね。
こちらは自作の、高3夏休み課題帳。

入試数学演習ⅠAⅡB/使用上の注意
1)解けなくてもすぐに答えを見ないこと。
2)この本の解答を、毎日読書すること。
3)1つの問題を、必ず2回は解くこと。
たった20問だけど、1問の中に多くの要素が含まれるよう問題を選んである。
冊子見本はこちら。塾は休業中。せっかく作ったのでどなたか活用ください。
数学の話。
定理や公式を証明することは、入試ではあまり出ないけど、証明をする過程の中に
結構重要な手法が隠れていることが、稀にある。

教科書を調べると、大体次のように垂線を引く。

これを見ると、三平方の定理と違うところが右辺の「-2cx」のところで、
bccosAはベクトルABとACの内積になることが発見できる。
また、逆にAHを求めたいときは、上の2行目の式をxについて解けばいい。
問1 Aが直角や鈍角の場合も成り立つことを確かめよ。
めんどくさくなったのか、こう書いてある教科書もありますね。
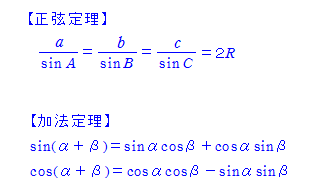
これらを使って余弦定理を導くことができるというので、考えてみた。

正弦・余弦定理は数学Ⅰ、加法定理は数学Ⅱなので、同時に学習できない。
なのでこの証明は日の目を見ることなく終わりそうですね。面白いのに残念。
また明日。
Posted by 三石 at 16:41│Comments(2)
│等式
この記事へのコメント
高3夏休み課題帳の12番の(1)は点(8,6)を通るように等号を入れますか?
東京は暑いですよね。お身体お厭いください。
東京は暑いですよね。お身体お厭いください。
Posted by 白 at 2019年08月15日 18:57
白様
ご指摘ありがとうございます
等号が抜けていてこれでは解けませんね。修正済
明日から避暑に行く予定。
ご指摘ありがとうございます
等号が抜けていてこれでは解けませんね。修正済
明日から避暑に行く予定。
Posted by task at 2019年08月15日 21:28
at 2019年08月15日 21:28
 at 2019年08月15日 21:28
at 2019年08月15日 21:28