2020年01月16日
2020日本数学オリンピック予選(問題1・2)
こんにちは。
今年で終了となるセンター試験は明後日。
数学は計算力重視で時間攻めという試験で、つまらなかった。
共通テストに代われば面白くなるかなと期待していたのだけど、
試行テストを見た限り、(こちら)
暗雲立ち込めるという感・・。
毎年この時期に行われるJMO予選。
面白い問が出てます。解けそうなもののみ解いてみますか。
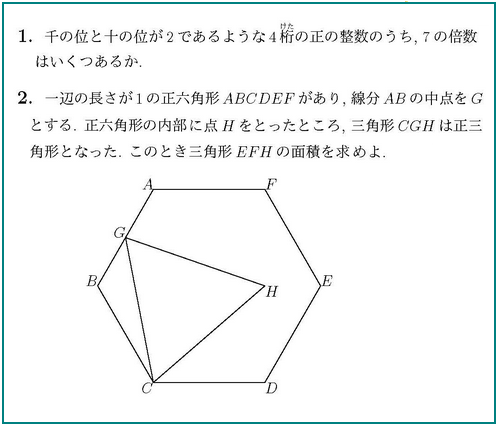
問1
7の倍数の見つけ方は知らないので、さてどうしますか?
位を別々にして7で割って余りを集める、という感じです。
問2
△EFHの底辺をEFとするか、HEとするか?
いくつか解き方がありそうです。
今年で終了となるセンター試験は明後日。
数学は計算力重視で時間攻めという試験で、つまらなかった。
共通テストに代われば面白くなるかなと期待していたのだけど、
試行テストを見た限り、(こちら)
暗雲立ち込めるという感・・。
毎年この時期に行われるJMO予選。
面白い問が出てます。解けそうなもののみ解いてみますか。

問1
7の倍数の見つけ方は知らないので、さてどうしますか?
位を別々にして7で割って余りを集める、という感じです。
問2
△EFHの底辺をEFとするか、HEとするか?
いくつか解き方がありそうです。

第1問なので素早く解きたいところ。

あとで気づいたのだけど、CDの中点をIとすると
四角形HIDEが平行四辺形になるようです。
この方法のが簡単だったかな。
また明日。
2025日本数学オリンピック予選(問題5)
2025日本数学オリンピック予選(問題4)
2025日本数学オリンピック予選(問題3)
2025日本数学オリンピック予選(問題1・2)
2024日本数学オリンピック予選(問題9)
2024日本数学オリンピック予選(問題8)
2025日本数学オリンピック予選(問題4)
2025日本数学オリンピック予選(問題3)
2025日本数学オリンピック予選(問題1・2)
2024日本数学オリンピック予選(問題9)
2024日本数学オリンピック予選(問題8)
Posted by 三石 at 22:22│Comments(2)
│JMO
この記事へのコメント
簡単すぎ
オリンピックって言うくらいだから、もっと難しいと思ったのに残念です。オリンピックを舐めないでください。
オリンピックって言うくらいだから、もっと難しいと思ったのに残念です。オリンピックを舐めないでください。
Posted by 大川 たかし at 2022年03月14日 13:47
Thanks for sharing the JMO.
For 問2, it seems much easier (yet less elegant), if handled by Complex Number in Euler Form. Resulting in H = 1/2. Then remaining straightforward.
For 問2, it seems much easier (yet less elegant), if handled by Complex Number in Euler Form. Resulting in H = 1/2. Then remaining straightforward.
Posted by naka at 2022年03月20日 01:17









