2019年08月04日
早く家に帰るには?
こんにちは。
8月に入り、ここ東京は連日の猛暑日。ただただ暑い・・。
こんな夏は避暑に長野へ帰るのがいいのだけど、長野も暑いようだ。
「身近な所で数学を使って物事を解決する、こういう問題を作ってほしい。」
という依頼が来ていて困っている。こんなものなかなか無いですよ・・。
身近な所に数学が生かせるのだから、数学を勉強する意味があるでしょ?
などと言うのは綺麗ごとであって、数学に興味を持つ生徒など増えやしない。
問題を解く中でのちょっとした考え方が、実生活のちょっとしたことに
関連しているな、と思うことはある。見えないところで役に立っている。
でも数学で一番大切なことはと言えば・・
問題を解くこと考えることが、面白い。
こう思えるかどうかですかね。
そのような問題をいま必死に作っているが・・今日は息抜きでパズルを1つ。
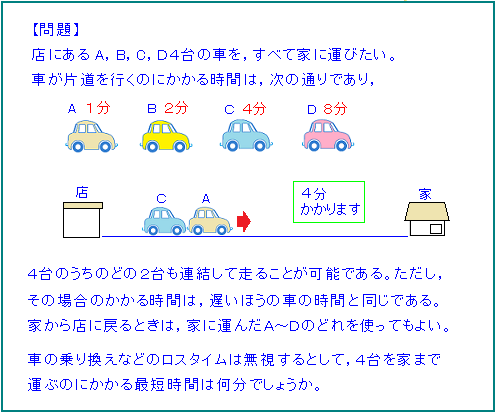
どのパズルの本にも大体載っている、有名なやつです。
(答)16分かと思いきや、答えは15分。
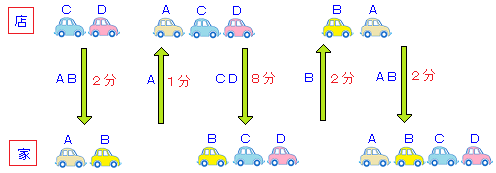
家から店に戻る2回をAでやると、合計16分ですが、
Bを家に置いておき、CDで行ってBで戻るというテクを使うと、15分になります。
設定時間を変えた場合、どうなるか?
これを論理的に考えてみました。

a、b、c、dの時間によって、答えが変わるのかどうか?
ここからはパズルでなく、数学の問題ですね。
8月に入り、ここ東京は連日の猛暑日。ただただ暑い・・。
こんな夏は避暑に長野へ帰るのがいいのだけど、長野も暑いようだ。
「身近な所で数学を使って物事を解決する、こういう問題を作ってほしい。」
という依頼が来ていて困っている。こんなものなかなか無いですよ・・。
身近な所に数学が生かせるのだから、数学を勉強する意味があるでしょ?
などと言うのは綺麗ごとであって、数学に興味を持つ生徒など増えやしない。
問題を解く中でのちょっとした考え方が、実生活のちょっとしたことに
関連しているな、と思うことはある。見えないところで役に立っている。
でも数学で一番大切なことはと言えば・・
問題を解くこと考えることが、面白い。
こう思えるかどうかですかね。
そのような問題をいま必死に作っているが・・今日は息抜きでパズルを1つ。

どのパズルの本にも大体載っている、有名なやつです。
(答)16分かと思いきや、答えは15分。

家から店に戻る2回をAでやると、合計16分ですが、
Bを家に置いておき、CDで行ってBで戻るというテクを使うと、15分になります。
設定時間を変えた場合、どうなるか?
これを論理的に考えてみました。

a、b、c、dの時間によって、答えが変わるのかどうか?
ここからはパズルでなく、数学の問題ですね。

一番遅いDが何分でも関係なく、
2番目のBが、A寄りか、C寄りか?
これによって方法が変わるというわけです。
なかなか面白い結果になったでしょう。
また明日。
Posted by 三石 at 19:48│Comments(0)
│等式