2019年07月20日
共分散とか相関係数とか。
こんにちは。
数学の問題を作る仕事をしている。
数学が好きで面白いと思うからやっているのだけど、簡単でなく労多いです。
「問題を作ってほしい。データの分析の・・」
この分野は高校の数学Ⅰの中に最近入り込んできて、センター試験にも
結構ページ数を割いている。作問が大変なので執筆者が少ないのだとか・・。
私だって、同じこと。

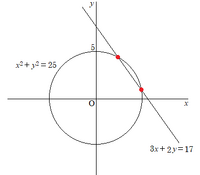
これは、作問したがボツになった図。
偏差=値-平均
分散=(偏差の2乗)の平均
共分散=「(Xの偏差)・(Yの偏差)」の平均
そして、

何なのか意味がわからないが、これらは暗記するしかない。
相関係数は-1から1までの値を取ることが、教科書に載ってます。
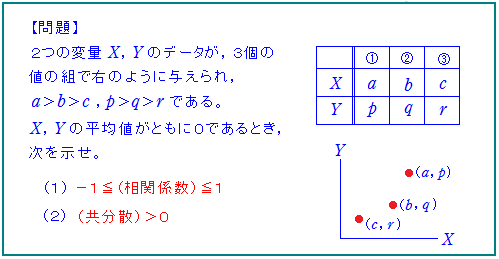
2019明治大・改
教科書に載っていることをあえて証明させる。
こういう入試問題もたまにありますね。良いと思う。
この2問の証明は、実に奥が深いです。
数学の問題を作る仕事をしている。
数学が好きで面白いと思うからやっているのだけど、簡単でなく労多いです。
「問題を作ってほしい。データの分析の・・」
この分野は高校の数学Ⅰの中に最近入り込んできて、センター試験にも
結構ページ数を割いている。作問が大変なので執筆者が少ないのだとか・・。
私だって、同じこと。

これは、作問したがボツになった図。
偏差=値-平均
分散=(偏差の2乗)の平均
共分散=「(Xの偏差)・(Yの偏差)」の平均
そして、

何なのか意味がわからないが、これらは暗記するしかない。
相関係数は-1から1までの値を取ることが、教科書に載ってます。

2019明治大・改
教科書に載っていることをあえて証明させる。
こういう入試問題もたまにありますね。良いと思う。
この2問の証明は、実に奥が深いです。

(2)は、
共分散 ≧(Xの平均)・(Yの平均)
という公式になります。
違う分野のことがこんなふうに結びついている。
こういうところが数学の面白さの1つかな。
それを踏まえての出題だとすれば、明治大さすがだ。
また明日。
Posted by 三石 at 18:58│Comments(0)
│等式