2017年12月15日
三角関数「加法定理」の証明。
こんにちは。
高2生「三角関数」の授業にて。
加法定理
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
これが一般角で成り立つことを証明するのは結構難しい。
以前東大の入試で出ましたね。こちら。
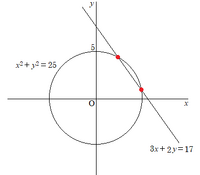
学校の授業でこういう図を描いて証明したよと、生徒が言ってきた。
確かこんな図だったと思う。

なかなかめんどい・・。
検索してみると、証明法いろいろ出てきますね。

このシンプルな図で、導けるかどうか・・?
これを考えてみた。
高2生「三角関数」の授業にて。
加法定理
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
これが一般角で成り立つことを証明するのは結構難しい。
以前東大の入試で出ましたね。こちら。
学校の授業でこういう図を描いて証明したよと、生徒が言ってきた。
確かこんな図だったと思う。

なかなかめんどい・・。
検索してみると、証明法いろいろ出てきますね。

このシンプルな図で、導けるかどうか・・?
これを考えてみた。

何とか出ましたね。
公式は暗記するだけでなく成り立つ訳も知っておくと、きっと視野が広くなると思う。
αやβが一般角の場合はどう証明するか?
教科書には単位円の周上に2点をとって、その距離から求める方法が載っている。
あとはベクトルの内積とか、行列とか複素数平面とか。
あまりネットに出ていない方法を紹介します。

いろいろあって、実に奥が深い。
また明日。
Posted by 三石 at 21:24│Comments(0)
│等式