2015年09月13日
組合せ論入門。
こんにちは。
数学書の紹介を1つ。
1985年初版。なのでずいぶんと年季のある風貌ですな。

大学のときの教科書だったけど、無くしてしまったのでamazonで再度購入した。
当時、こういう数学もあるのかと興味を持った。私の専門は幾何だったけどまったく
つまらなかったので、組合せ論、というかグラフ理論を結構勉強していた。
この本、組合せ論の入門書として随分わかりやすいし、掲載の例題が身近な物なので、
興味深くて面白い。背理法と帰納法がわかる高校生なら楽しく読めると思う。
組合せ論にありがちな問を1つ。

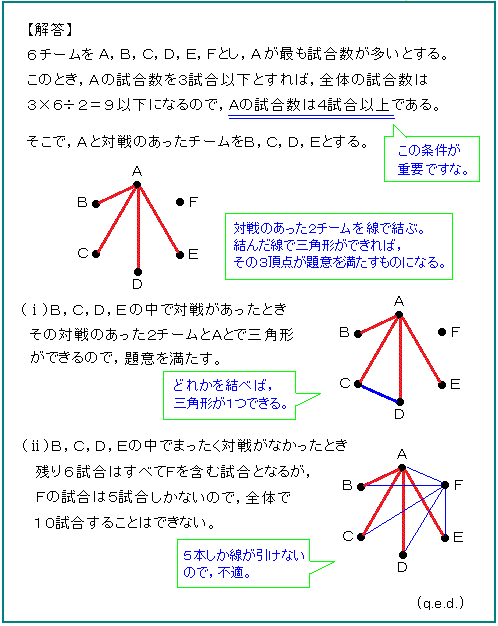
対戦のあったチームどうしを線で結んだ図をかいて、その中に三角形ができれば、
その3つの頂点が求めたいものになる。そういう考え方で証明します。
数学書の紹介を1つ。
1985年初版。なのでずいぶんと年季のある風貌ですな。

大学のときの教科書だったけど、無くしてしまったのでamazonで再度購入した。
当時、こういう数学もあるのかと興味を持った。私の専門は幾何だったけどまったく
つまらなかったので、組合せ論、というかグラフ理論を結構勉強していた。
この本、組合せ論の入門書として随分わかりやすいし、掲載の例題が身近な物なので、
興味深くて面白い。背理法と帰納法がわかる高校生なら楽しく読めると思う。
組合せ論にありがちな問を1つ。

対戦のあったチームどうしを線で結んだ図をかいて、その中に三角形ができれば、
その3つの頂点が求めたいものになる。そういう考え方で証明します。
これの元ネタは、次です。
頂点が2N個、辺がN^2+1本のグラフでは、その中に三角形が必ず存在する。
これを証明せよ。
興味のある方、解いてみてください。
また明日。
Posted by 三石 at 21:43│Comments(0)
│集合
※このブログではブログの持ち主が承認した後、コメントが反映される設定です。









