2010年11月30日
2乗の計算。
こんにちは。
11月も今日で終わり。
今年もあと1か月ですね。
首輪のヒモが切れてしまったようです。

すまし込んでますが、さっきまで脱走しておりました。
近所から捕獲したとのTELあり。よかったです・・。
数字の並びで面白い性質を見つけました。

同じ数の並びは、次のように分数式で表せます。

右辺の分子は999・・・9だから、これを9で割れば左辺と同じことです。
これを使って式で表して証明する感じです。
やや、ややこしい。
続きを読む
11月も今日で終わり。
今年もあと1か月ですね。
首輪のヒモが切れてしまったようです。

すまし込んでますが、さっきまで脱走しておりました。
近所から捕獲したとのTELあり。よかったです・・。
数字の並びで面白い性質を見つけました。
同じ数の並びは、次のように分数式で表せます。
右辺の分子は999・・・9だから、これを9で割れば左辺と同じことです。
これを使って式で表して証明する感じです。
やや、ややこしい。
続きを読む
2010年11月26日
魔方陣(3×3)の巻。
こんにちは。
これは干し大根。

出荷をし1本130円ほどの売り上げになる。
売れ残る不恰好なものほど、うまいとか。
魔方陣の研究その1。
タテ、ヨコ、ナナメのどの3つを足しても15になります。

3×3の場合、回転や反転を除くとこの1通りしかありません。
この数字を代えるとどうなるか・・。

うまい探し方を、したいところ。
続きを読む
これは干し大根。

出荷をし1本130円ほどの売り上げになる。
売れ残る不恰好なものほど、うまいとか。
魔方陣の研究その1。
タテ、ヨコ、ナナメのどの3つを足しても15になります。
3×3の場合、回転や反転を除くとこの1通りしかありません。
この数字を代えるとどうなるか・・。
うまい探し方を、したいところ。
続きを読む
2010年11月23日
座席の交換。
こんにちは。
とある会食の席に呼ばれました。

市内の日本料理の店。
次々と珍しい和食が出ました。おいしかった。
座席に名札が置いてあったのを知らずに、違うとこに座ってしまった。
それで、こういう問いが浮かんだ・・。

何をもって証明とするのか、困りますね。
N人のときの数学的帰納法。これで行きました。
続きを読む
とある会食の席に呼ばれました。

市内の日本料理の店。
次々と珍しい和食が出ました。おいしかった。
座席に名札が置いてあったのを知らずに、違うとこに座ってしまった。
それで、こういう問いが浮かんだ・・。
何をもって証明とするのか、困りますね。
N人のときの数学的帰納法。これで行きました。
続きを読む
2010年11月19日
2010年11月18日
第197回数検1級・1次(問題6)
こんにちは。
微分・積分っていったい何ですか?
微分とは、微(かす)かに分かる。
積分とは、分かった積もり。
誰の迷言でしょうか・・。
取り急ぎ、6問目です。

積分がうまく行かないときは文字で置き換えるのが手ですが、
tanx=yとおくか、
または全体をyとおくか。
どちらにしても簡単に行きません。
解答は、間違えてxをθにしてしまってます。
続きを読む
微分・積分っていったい何ですか?
微分とは、微(かす)かに分かる。
積分とは、分かった積もり。
誰の迷言でしょうか・・。
取り急ぎ、6問目です。
積分がうまく行かないときは文字で置き換えるのが手ですが、
tanx=yとおくか、
または全体をyとおくか。
どちらにしても簡単に行きません。
解答は、間違えてxをθにしてしまってます。
続きを読む
2010年11月16日
第197回数検1級・1次(問題5)
こんにちは。
さいころの話。

昔、ピンゾロの丁と言ったそうです。
これが出るまで、さいころを何回振ることになるか?
3度実験したところ、
1試技目 26回
2試技目 19回
3試技目 40回振ったが出ず。
まちまちですね。
平均回数=1÷(確率)
という公式があって、平均回数は36回。つまり、
試技をたくさんやれば、アベレージが36に近づく
ということが言えます。
引き続き実験をおこないたいが、疲れてしまった・・。
数検1級5問目です。

分散というのは散らばりの度合いを表す数値で、求め方はすごく面倒・・。
(分散)=(2乗の平均)-(平均の2乗)
と暗記しておくといいです。
続きを読む
さいころの話。

昔、ピンゾロの丁と言ったそうです。
これが出るまで、さいころを何回振ることになるか?
3度実験したところ、
1試技目 26回
2試技目 19回
3試技目 40回振ったが出ず。
まちまちですね。
平均回数=1÷(確率)
という公式があって、平均回数は36回。つまり、
試技をたくさんやれば、アベレージが36に近づく
ということが言えます。
引き続き実験をおこないたいが、疲れてしまった・・。
数検1級5問目です。
分散というのは散らばりの度合いを表す数値で、求め方はすごく面倒・・。
(分散)=(2乗の平均)-(平均の2乗)
と暗記しておくといいです。
続きを読む
2010年11月13日
第197回数検1級・1次(問題4)
こんにちは。
小中学生の何かのキャンペーンなのか、
ポスターの優秀作品が展示されていました。

構図といい色彩といい、見事ですな。
こういうセンスがあること。うらやましい。
数検1級の4問目です。

固有値というのは、
AP=xP (Pは零ベクトルでない)
となる実数xのことです。
このxの求め方は、
A-xE (Eは単位行列)
これの行列式を計算して0になるxを求める。
もう、丸暗記ですな。
続きを読む
小中学生の何かのキャンペーンなのか、
ポスターの優秀作品が展示されていました。

構図といい色彩といい、見事ですな。
こういうセンスがあること。うらやましい。
数検1級の4問目です。
固有値というのは、
AP=xP (Pは零ベクトルでない)
となる実数xのことです。
このxの求め方は、
A-xE (Eは単位行列)
これの行列式を計算して0になるxを求める。
もう、丸暗記ですな。
続きを読む
2010年11月11日
第197回数検1級・1次(問題3)
こんにちは。
極限の話。
級数というのは、数を無限に足していったその和のことで、
収束というのは、この和が1つの数に落ち着くこと、を言います。
数検1級の3問目です。

大学1年の解析学という分野。
公式を知っていれば難しくないが、知らないとお手上げです。

見づらいですが、この3つを使います。
続きを読む
極限の話。
級数というのは、数を無限に足していったその和のことで、
収束というのは、この和が1つの数に落ち着くこと、を言います。
数検1級の3問目です。
大学1年の解析学という分野。
公式を知っていれば難しくないが、知らないとお手上げです。

見づらいですが、この3つを使います。
続きを読む
2010年11月10日
第197回数検1級・1次(問題2)
こんにちは。
こういう季節が来ましたね。

市田柿というブランドの干し柿。
完成は来月中旬でしょうか。うまいですよ。
数検1級のつづき。

複2次式という式で、これはまず2乗を文字で置き換えます。
そのあと1を入れると0になるので、とりあえず
(x-1)(x+1)×(4次式)
となります。
あとは4次式のところがたぶん因数分解できるでしょう。
続きを読む
こういう季節が来ましたね。
市田柿というブランドの干し柿。
完成は来月中旬でしょうか。うまいですよ。
数検1級のつづき。
複2次式という式で、これはまず2乗を文字で置き換えます。
そのあと1を入れると0になるので、とりあえず
(x-1)(x+1)×(4次式)
となります。
あとは4次式のところがたぶん因数分解できるでしょう。
続きを読む
2010年11月08日
第197回数検1級・1次(問題1)
こんにちは。
昨日行われたもようの数学検定。
受検されたかた、いかがでしたか。

私は2年前の11月に受けました。写真はそのときの激戦のようす。
1級1次は60分間で7問もあり、2問落としたら不合格です。
時間が無いのがキツいのと、計算スペースが無いのがキツい。

(注)数検協会の許可を得て掲載しています。
因数分解してパターンを列挙するタイプです。
331が素数かどうかを調べるには、√331以下の奇数
3、5、7、11、13、17
これで割れるかどうかを見ます。
どれも割れないのでラッキーな展開。
続きを読む
昨日行われたもようの数学検定。
受検されたかた、いかがでしたか。

私は2年前の11月に受けました。写真はそのときの激戦のようす。
1級1次は60分間で7問もあり、2問落としたら不合格です。
時間が無いのがキツいのと、計算スペースが無いのがキツい。
(注)数検協会の許可を得て掲載しています。
因数分解してパターンを列挙するタイプです。
331が素数かどうかを調べるには、√331以下の奇数
3、5、7、11、13、17
これで割れるかどうかを見ます。
どれも割れないのでラッキーな展開。
続きを読む
2010年11月07日
ドーム菊。
こんにちは。
どうでしょう。

見事なドーム型。
丸く咲くような細工があるのでしょうかね・・。
球の体積。
公式を忘れたときどうするか。こういう手があります。
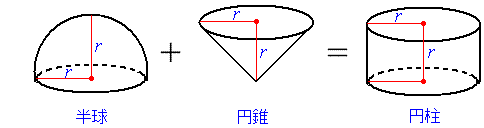
半球と円錐の体積の和は、円柱の体積に等しくなります。
なぜなら、下から高さxのところで切り取った面の面積を調べると、

このように等しくなるので、これを0からrまで積分してやれば、
体積も等しくなるというわけです。
この結果、球の体積はどうなるか・・?
続きを読む
どうでしょう。

見事なドーム型。
丸く咲くような細工があるのでしょうかね・・。
球の体積。
公式を忘れたときどうするか。こういう手があります。
半球と円錐の体積の和は、円柱の体積に等しくなります。
なぜなら、下から高さxのところで切り取った面の面積を調べると、
このように等しくなるので、これを0からrまで積分してやれば、
体積も等しくなるというわけです。
この結果、球の体積はどうなるか・・?
続きを読む
2010年11月05日
大福と草餅
こんばんは。
ひと息、メンテナンス中。

赤い部分を回すとインクが吸い上がってきます。
こういう面倒なところがまた楽し。

書き味、抜群ですな。
明後日は数学検定ですね。2次試験対策の問題を作りました。

10分で3級・・くらい。
こんな問題、絶対出ないか・・。
続きを読む
ひと息、メンテナンス中。

赤い部分を回すとインクが吸い上がってきます。
こういう面倒なところがまた楽し。

書き味、抜群ですな。
明後日は数学検定ですね。2次試験対策の問題を作りました。
10分で3級・・くらい。
こんな問題、絶対出ないか・・。
続きを読む



