2016年01月17日
２０１６日本数学オリンピック予選（問題３）
こんにちは。
センター試験終わりましたね。
早速、解かねば・・。
JMOはしばし休みです。
正確な図がうまく描けないが、こんな感じになる。
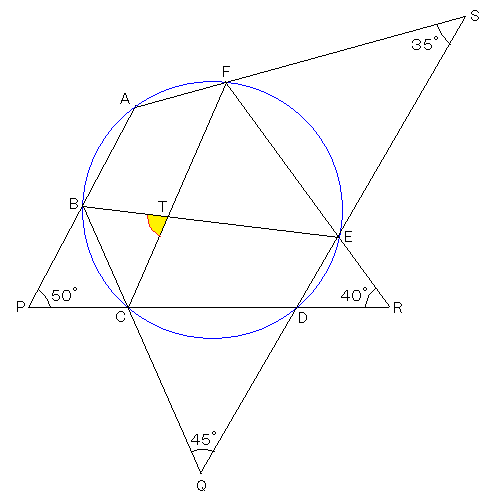
三角形の内角の和は１８０°
内接四角形の対角の和は１８０°
円周角の定理（＝同じ弧に対する円周角は等しい）
この３つを使えば解けるはず。あとはどう補助線を引くかです。
センター試験終わりましたね。
早速、解かねば・・。
JMOはしばし休みです。
正確な図がうまく描けないが、こんな感じになる。
三角形の内角の和は１８０°
内接四角形の対角の和は１８０°
円周角の定理（＝同じ弧に対する円周角は等しい）
この３つを使えば解けるはず。あとはどう補助線を引くかです。
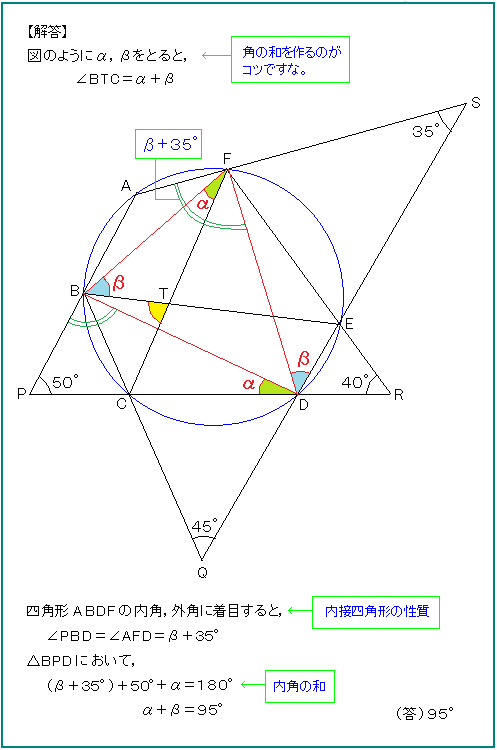
QとRは全く使わなくて解けた。
ダミーだったようですね。
また明日。
２０２５日本数学オリンピック予選（問題５）
２０２５日本数学オリンピック予選（問題４）
２０２５日本数学オリンピック予選（問題３）
２０２５日本数学オリンピック予選（問題１・２）
２０２４日本数学オリンピック予選（問題９）
２０２４日本数学オリンピック予選（問題８）
２０２５日本数学オリンピック予選（問題４）
２０２５日本数学オリンピック予選（問題３）
２０２５日本数学オリンピック予選（問題１・２）
２０２４日本数学オリンピック予選（問題９）
２０２４日本数学オリンピック予選（問題８）
Posted by 三石 at 18:16│Comments(2)
│JMO
この記事へのコメント
こんな簡単にできるのですね。
私は、考え抜いた挙句、BFとABの延長線上の交点を作るやりかたでやってしまいました。
私は、考え抜いた挙句、BFとABの延長線上の交点を作るやりかたでやってしまいました。
Posted by ti at 2016年01月28日 07:47
tiさん
BAとEFを延長して新たに三角形を作るのでしょうか？
後日解いてみようと思います。
BAとEFを延長して新たに三角形を作るのでしょうか？
後日解いてみようと思います。
Posted by task
at 2016年01月30日 15:46
at 2016年01月30日 15:46※このブログではブログの持ち主が承認した後、コメントが反映される設定です。
＜ご注意＞
書き込まれた内容は公開され、ブログの持ち主だけが削除できます。 |
