2015年03月03日
東大２０１５・理系（第５問）
こんにちは。
国立大２次試験が終了。
いま東大の全１０問すべて解き終わりました。
流石に思考力を問う良問揃いといった感じです。
理系（理科）の６問のうち、次の第５問が考えにくかったと思う。
これを捨て問にした人、多かったかもしれない。
解けなかったとしても、とりあえず図のようにｍ＝１からｍ＝７くらいまで
書き出すことはしてほしい。こういう労力を惜しんではいけない。
実際、この図を見ていて解法が浮かんだ・・。
国立大２次試験が終了。
いま東大の全１０問すべて解き終わりました。
流石に思考力を問う良問揃いといった感じです。
理系（理科）の６問のうち、次の第５問が考えにくかったと思う。
これを捨て問にした人、多かったかもしれない。
解けなかったとしても、とりあえず図のようにｍ＝１からｍ＝７くらいまで
書き出すことはしてほしい。こういう労力を惜しんではいけない。
実際、この図を見ていて解法が浮かんだ・・。
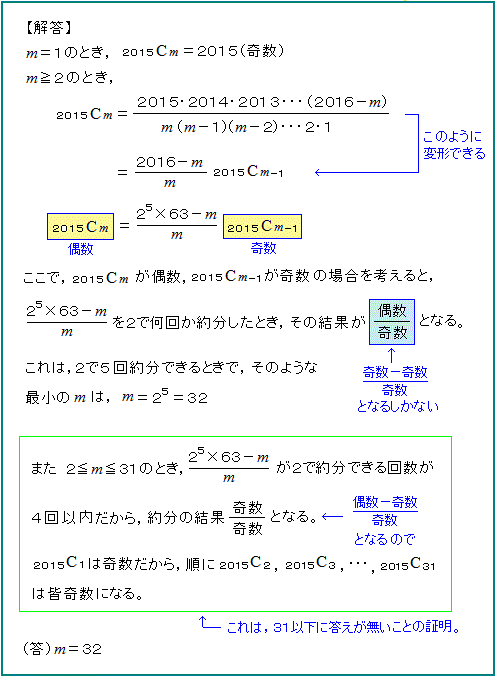
某予備校サイトにもっと簡潔でうまい解法が載ってますね。
そちらを参照されたし・・。
また明日。
Posted by 三石 at 21:17│Comments(2)
│入試
この記事へのコメント
お久しぶりです。
今回の問題、2016が32の倍数であり64の倍数ではないことがミソのように思えました。
分母は1から昇順にm個、分子は2015から降順にm個を掛けあわせるので、2016が32の倍数であることと倍数の並びの規則性を考慮すると、2,4,8,16,32の倍数は分母と分子に同じ数ずつ掛け合わされている。だから、約分で素因数2が過不足なく相殺されて奇数になってしまう。
ところが、2015から降順に数えて32番目の1984は64の倍数なので、ここで素因数2の個数に差が出る（分子の方が1つだけ多くなる）から、初めて約分後も偶数になる。
・・・という理解でいいのでしょうか。このまま解答として書き上げるのは大変ですが・・・。
今回の問題、2016が32の倍数であり64の倍数ではないことがミソのように思えました。
分母は1から昇順にm個、分子は2015から降順にm個を掛けあわせるので、2016が32の倍数であることと倍数の並びの規則性を考慮すると、2,4,8,16,32の倍数は分母と分子に同じ数ずつ掛け合わされている。だから、約分で素因数2が過不足なく相殺されて奇数になってしまう。
ところが、2015から降順に数えて32番目の1984は64の倍数なので、ここで素因数2の個数に差が出る（分子の方が1つだけ多くなる）から、初めて約分後も偶数になる。
・・・という理解でいいのでしょうか。このまま解答として書き上げるのは大変ですが・・・。
Posted by HAMAH at 2015年03月04日 20:03
HAMAHさん
お久しぶりです。流石にうまいですね。
調べてみるとこの問にはいろいろと背景があるようで、結構学ぶものありました。
お久しぶりです。流石にうまいですね。
調べてみるとこの問にはいろいろと背景があるようで、結構学ぶものありました。
Posted by task
at 2015年03月07日 00:54
at 2015年03月07日 00:54※このブログではブログの持ち主が承認した後、コメントが反映される設定です。
