三石・数学塾

こんにちは。

数学Ⅲの原稿を書いているのだけど、「極座標」のところやりにくい。
今１つ実用性が伝わりにくいところだ・・。

「正葉曲線」というのは、次のようなシンプルな極方程式で表される。



実に面白い曲線を描きますよね。sinでなくcosの場合も正葉曲線になる。
いろいろとネットで調べていたら、こういう入試問題にあたった。


２０１８東京医科大


これ、どうやって解くのだろーか？
yについて解いて微分するなど不可能だし、媒介変数を使うのも複雑になる。

ところが極座標にするとシンプルになるのだから、それを狙った出題のようだ・・。

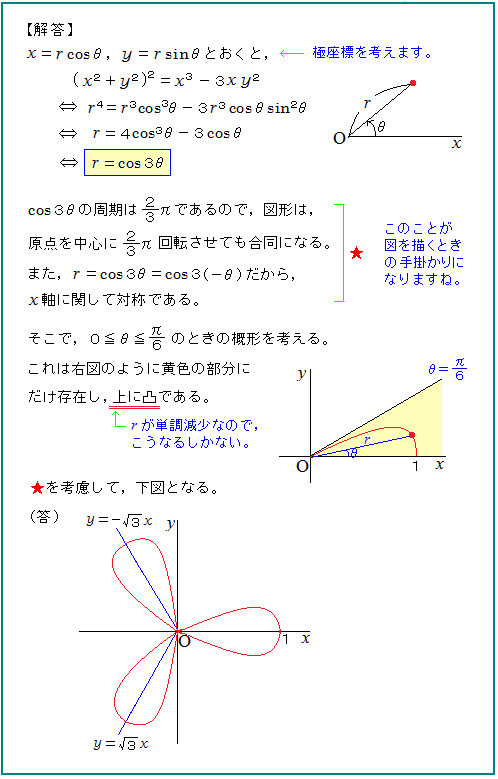
極座標のままで正確な図を描くのは、相当な無理がある。
この程度の解説と図示で、点がもらえるでしょうかね・・？

極値を出してないと減点！！
凹凸をしっかり吟味してないと減点！！

こんな細かいこと言うのなら、そんな大学など受験やめよう。

また明日。