2016年07月31日
夏休み課題その3
こんにちは。
数学ができるようになる為にどう勉強すればよいか?
(1)すぐに答えを見ない。
(2)昨日の解答を眺める。
私はこの2点だと思っていて、生徒にいつも言っている。

(1)は自力で答えを出す努力をすることが思考力を伸ばす力になる。
(2)はノートに書いた解答をあとで見返すことで、忘れなくする効果と、
新たな発見があったりする利点がある。見直しは必ずするべし。
写真は三石ノートという物で全10巻あり。数学にもノート整理は効果大。
夏休み課題その3。

これはネットで検索すれば解法がたくさん出てくる有名な問い。
高校3年間のうちに一度は解いておかねばならない重要問題といえます。
数学ができるようになる為にどう勉強すればよいか?
(1)すぐに答えを見ない。
(2)昨日の解答を眺める。
私はこの2点だと思っていて、生徒にいつも言っている。

(1)は自力で答えを出す努力をすることが思考力を伸ばす力になる。
(2)はノートに書いた解答をあとで見返すことで、忘れなくする効果と、
新たな発見があったりする利点がある。見直しは必ずするべし。
写真は三石ノートという物で全10巻あり。数学にもノート整理は効果大。
夏休み課題その3。

これはネットで検索すれば解法がたくさん出てくる有名な問い。
高校3年間のうちに一度は解いておかねばならない重要問題といえます。
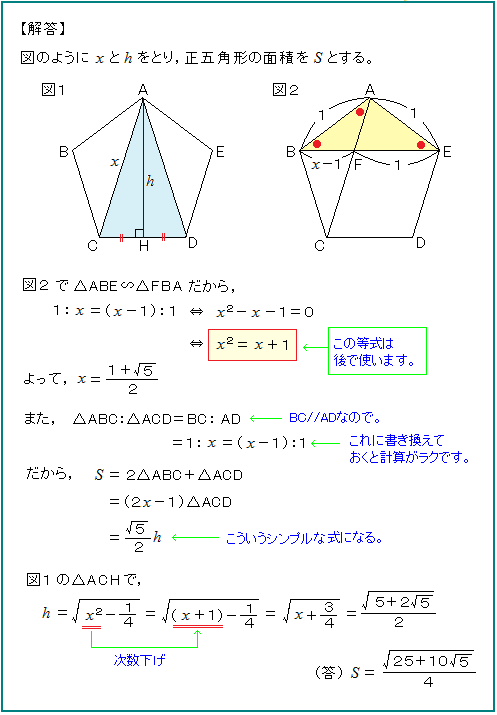
解き方はいろいろあって、中心を取り5個の二等辺に分けるとか、
先に三角比を求めてしまう方法もあるし、なかなか深いです。
また明日。
Posted by 三石 at 03:08│Comments(11)
│幾何
この記事へのコメント
全体 KARA 「抜く」発想がイイ と 積分で;
Pi*(Sqrt[1/10 (5 + Sqrt[5])])^2 ひくっ
5*Integrate[
Sqrt[5 + Sqrt[5] - 10 x^2]/Sqrt[
10] - (-((
Sqrt[2/(5 + Sqrt[
5])] (-2 Sqrt[5 (5 + 2 Sqrt[5])] +
5 Sqrt[2 (3 + Sqrt[5])] x))/(5 (-1 + Sqrt[5])))), {x,
1/4 (-1 + Sqrt[5]) Sqrt[1/10 (5 + Sqrt[5])], Sqrt[
1/10 (5 + Sqrt[5])]}]
=1/4 Sqrt[5 (5 + 2 Sqrt[5])]
Pi*(Sqrt[1/10 (5 + Sqrt[5])])^2 ひくっ
5*Integrate[
Sqrt[5 + Sqrt[5] - 10 x^2]/Sqrt[
10] - (-((
Sqrt[2/(5 + Sqrt[
5])] (-2 Sqrt[5 (5 + 2 Sqrt[5])] +
5 Sqrt[2 (3 + Sqrt[5])] x))/(5 (-1 + Sqrt[5])))), {x,
1/4 (-1 + Sqrt[5]) Sqrt[1/10 (5 + Sqrt[5])], Sqrt[
1/10 (5 + Sqrt[5])]}]
=1/4 Sqrt[5 (5 + 2 Sqrt[5])]
Posted by ★ at 2016年08月09日 23:34
5*(Sqrt[1/10 (5 + Sqrt[5])]*
Cos[(1/2)*((2*Pi)/5)]*(Sqrt[1/10 (5 + Sqrt[5])]*
Sin[(1/2)*((2*Pi)/5)]))
= 1/4 Sqrt[5 (5 + 2 Sqrt[5])]
とも。
Cos[(1/2)*((2*Pi)/5)]*(Sqrt[1/10 (5 + Sqrt[5])]*
Sin[(1/2)*((2*Pi)/5)]))
= 1/4 Sqrt[5 (5 + 2 Sqrt[5])]
とも。
Posted by ★ at 2016年08月10日 00:14
{{Sqrt[1/10 (5 + Sqrt[5])], 0},
{1/4 (-1 + Sqrt[5]) Sqrt[1/10 (5 + Sqrt[5])], Sqrt[
1/10 (5/8 + Sqrt[5]/8) (5 + Sqrt[5])]}}
の 行列式の 5*(1/2) で 1/4 Sqrt[5 (5 + 2 Sqrt[5])]
{1/4 (-1 + Sqrt[5]) Sqrt[1/10 (5 + Sqrt[5])], Sqrt[
1/10 (5/8 + Sqrt[5]/8) (5 + Sqrt[5])]}}
の 行列式の 5*(1/2) で 1/4 Sqrt[5 (5 + 2 Sqrt[5])]
Posted by ★ at 2016年08月10日 10:38
{{Sqrt[1/10 (5 + Sqrt[5])], 0},
{1/4 (-1 + Sqrt[5]) Sqrt[1/10 (5 + Sqrt[5])], Sqrt[
1/10 (5/8 + Sqrt[5]/8) (5 + Sqrt[5])]}}
の 行列式の 5*(1/2) で 1/4 Sqrt[5 (5 + 2 Sqrt[5])]
{1/4 (-1 + Sqrt[5]) Sqrt[1/10 (5 + Sqrt[5])], Sqrt[
1/10 (5/8 + Sqrt[5]/8) (5 + Sqrt[5])]}}
の 行列式の 5*(1/2) で 1/4 Sqrt[5 (5 + 2 Sqrt[5])]
Posted by ★ at 2016年08月10日 10:39
S=5/4tan(π/5) でもあってますよ
Posted by ぱーるゔぁlex at 2017年06月03日 23:37
........ね?
Posted by ぱーるゔぁlex at 2017年06月03日 23:37
僕が独自に導き出した大したことねー定理を使います。
(証明は後)
直径1の円に内接する正n角形の一辺長はsin(π/n)なので、まず直径は
sin(π/5):1=1:x
x=1/sin(π/5)
辺から外に伸びる二等分線の接点までをaとして、その接点から、辺の端までの長さをyとすると、大したことねー定理よりy=sin(π/10)なので三平方の定理より、
a^2+sin^2(π/5)/4=sin^2(π/10)
a=√(1-cos^2(π/10)/4cos^2(10)
=sin(π/10)/2cos(π/10)
そして、底辺を1として、半径からaを引いたものを高さとした三角形は正五角形の中に5個あるので、まず高さを求める。
1/{4sin(π/10)cos(π/10)}-{sin(π/10)/2cos(π/10)}
=cos(π/5)/(4sin(π/10)cos(π/10))
=cos(π/5)/2sin(π/5)
=1/2tan(π/5)
これに、底辺1をかけ、2で割って5をかけると、
5/4tan(π/5)
となり、求める結果が得られた。
(証明は後)
直径1の円に内接する正n角形の一辺長はsin(π/n)なので、まず直径は
sin(π/5):1=1:x
x=1/sin(π/5)
辺から外に伸びる二等分線の接点までをaとして、その接点から、辺の端までの長さをyとすると、大したことねー定理よりy=sin(π/10)なので三平方の定理より、
a^2+sin^2(π/5)/4=sin^2(π/10)
a=√(1-cos^2(π/10)/4cos^2(10)
=sin(π/10)/2cos(π/10)
そして、底辺を1として、半径からaを引いたものを高さとした三角形は正五角形の中に5個あるので、まず高さを求める。
1/{4sin(π/10)cos(π/10)}-{sin(π/10)/2cos(π/10)}
=cos(π/5)/(4sin(π/10)cos(π/10))
=cos(π/5)/2sin(π/5)
=1/2tan(π/5)
これに、底辺1をかけ、2で割って5をかけると、
5/4tan(π/5)
となり、求める結果が得られた。
Posted by ぱーるゔぁlex at 2017年06月04日 00:02
大したことねー定理の証明
単位円に内接する正n角形の一辺長をaとすると、三平方の定理より
a^2=sin^2(2π/n)+(1-cos(2π/n))^2
=2-2cos(2π/n)
なのでaは
a=√(2-2cos(2π/n))
=√2・√(1-cos(2π/n))
=√2・√2sin^2(π/n)
=2sin(π/n)
となる、つまり、直径を1にすると、
sin(π/n)
(ていうか本当は定理なんて大層な名前付けてもしょうがないと思うんですが他の定理の証明で使うので定理ちうことにしてます。)
単位円に内接する正n角形の一辺長をaとすると、三平方の定理より
a^2=sin^2(2π/n)+(1-cos(2π/n))^2
=2-2cos(2π/n)
なのでaは
a=√(2-2cos(2π/n))
=√2・√(1-cos(2π/n))
=√2・√2sin^2(π/n)
=2sin(π/n)
となる、つまり、直径を1にすると、
sin(π/n)
(ていうか本当は定理なんて大層な名前付けてもしょうがないと思うんですが他の定理の証明で使うので定理ちうことにしてます。)
Posted by ぱーるゔぁlex at 2017年06月04日 00:10
ぱーるゔぁlex さん
ずいぶん遠回りなやり方しますね。
中心から1辺に垂線を引くと36°の直角三角形ができるので、
この垂線の長さをhとして直接tanを使えば、
tan36°=1/(2h)
h=1/(2tan36°)
このhを使えば面積がすぐに出せるでしょう。
ずいぶん遠回りなやり方しますね。
中心から1辺に垂線を引くと36°の直角三角形ができるので、
この垂線の長さをhとして直接tanを使えば、
tan36°=1/(2h)
h=1/(2tan36°)
このhを使えば面積がすぐに出せるでしょう。
Posted by task at 2017年06月05日 12:51
at 2017年06月05日 12:51
 at 2017年06月05日 12:51
at 2017年06月05日 12:51うわっ本当だ。自分はやっぱりまだまだ未熟でした。
Posted by ぱーるゔぁlex at 2017年06月06日 16:33
あれ一般化したんですけど一辺が1の正n角形の面積はすべてn/(4tan π/n)でしt(nは整数)
Posted by ぱーるゔぁlex at 2017年06月06日 16:38